
EMAT6680 Assignment 8
Altitude Relationships
By Kevin Perry
Altitudes of
Triangles
In this discussion we will prove an interesting property of the altitudes of a triangle.
Definition
The altitude of a triangle at a particular vertex is defined as the line segment for the vertex to the opposite side that forms a perpendicular with the line through the other two vertices. The figure below shows a triangle and the altitude of the triangle through the point A
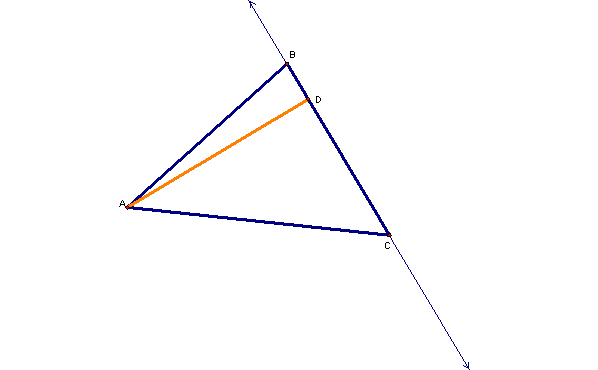
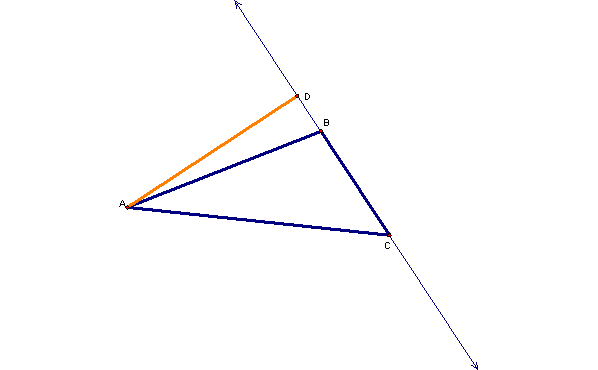
In this case, the triangle is acute, and the altitude is interior to the triangle. But the altitude is still defined the same way even if the triangle is obtuse, as shown below.
Altitudes and the
Orthocenter
If we construct all of the altitudes of a triangle, we get the following picture
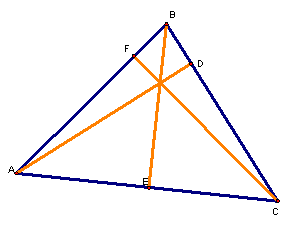
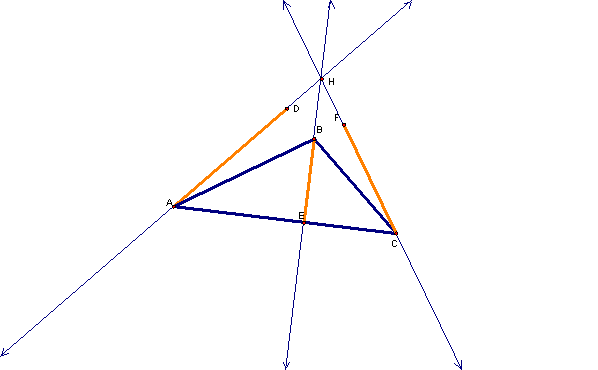
We notice that all three of the altitudes cross at a common point. This point is called the orthocenter of the triangle. It is usually labeled as H. Even if the triangle is obtuse, the lines containing the altitudes still intersect at a common point, as can be seen below.
The Orthocenter
and the Circumcircle
The circumcircle is the circle that contains all of the vertices of the triangle. If we add the circumcircle to the construction of the orthocenter, we can start seeing some new line segments appear.
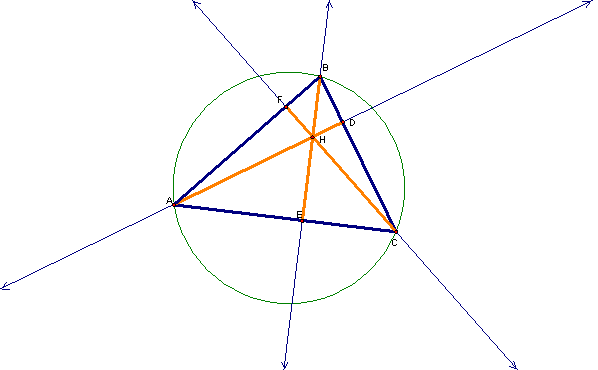
In particular, we see that there are “extended altitudes” that go from each vertex to the circumcircle and are still perpendicular to the opposite side. If we label those points of intersection, we get

We would like to see if there is any unique relationship concerning these “extended altitudes”.
Ratios of
Altitudes
Let’s look at the sum of the ratios of the true altitudes to the extended altitudes. In other words, what is
![]()
Empirically, we can calculate this result on GSP, as shown below.

What if the triangle is obtuse? Click on this GSP file and investigate.
This result is very surprising, so we need to prove why the result is 4.
Proof of the Sum
of the Altitude Ratios
The first step in our proof is to notice that if we reflect the orthocenter across any of the sides, we get the point on the circumcircle. As a example, if we reflect the segments AH and BH across the segment AB, we see that they intersect at point R, as shown below.
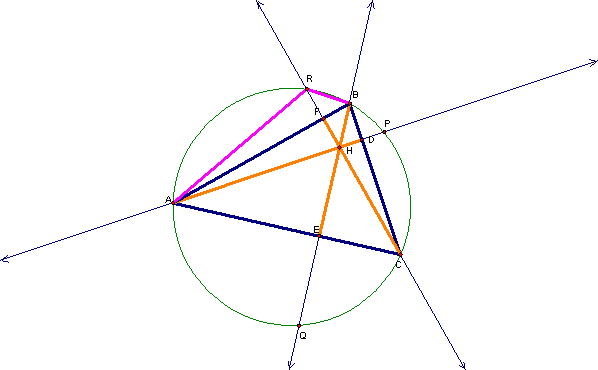
From the similar triangles, we see that HF = FR. Therefore, CR = CF + FR or CR = CF + HF. If we extend this for all of the altitudes, we get
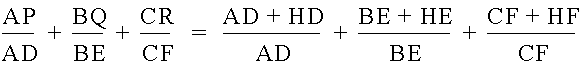
Which we see can be reduced to
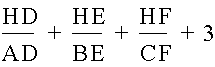
So our problem is now reduced to showing that
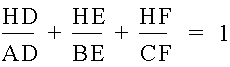
In other words, now we are concerned with the sum of the ratios of the distance of the orthocenter from each side related to the length of the altitude.
To help us with this proof, let’s again look at the triangle with its orthocenter, and the triangles that are formed by the altitudes.

From the picture we can see the similarity of the same-colored triangles. And these triangles are also similar to the larger triangles that contain three of the smaller triangles. The similarity is proven by the angles formed by the altitudes at the point H. For example, the angle EHC is the same as the angle FHB, and therefore the two green triangles are similar, because they are both right triangles and they have one other common angle. From all these similar triangles, we can write some equalities.
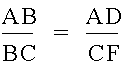
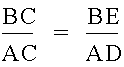
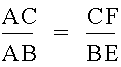
To begin the proof, we calculate the area of the triangle as
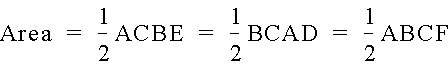
But the area can also be expressed ass the sum of the areas of the smaller triangles, AHC, AHB, and BHC, and therefore
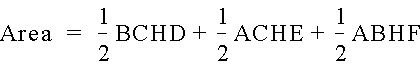
Substituting in the expressions from the similar triangles, we have
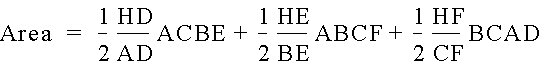
And setting the two equations equal and substituting for the products gives
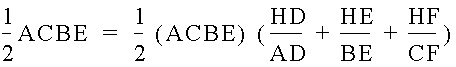
and dividing both sides by ACBE and ˝ gives
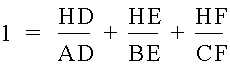
which is the desired result.
Therefore, we can see that the sum of the ratios of the extended altitudes to the altitudes is always 4.
Conclusions and
Extensions
The sum of the ratios of the “extended altitudes” to the altitudes is a fixed number (4) regardless of the triangle. The proof in this discussion is not the only way to prove this fact. Another method may analyze the interior angles that the triangle and its extended altitudes make in the circumcircle.
Also, there are other sums that can be found from this proof and also proven. A good example to try would be
![]()
This result should come easily from the main proof in this discussion.