
EMAT6680 Assignment 9
Pedal Triangles
By Kevin Perry
Pedal Triangles
In this discussion we will investigate the special triangle called a pedal triangle.
Constructing a
Pedal Triangle
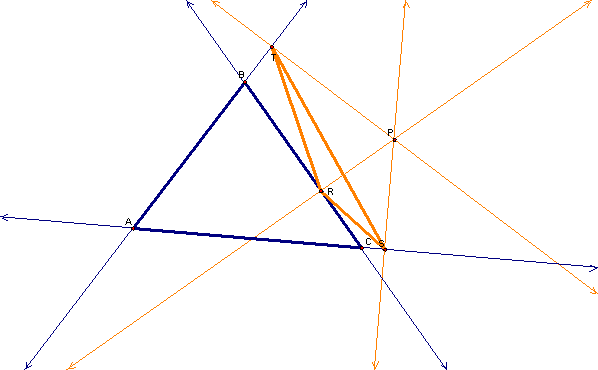
The first thing we need to do in this discussion is to construct a pedal triangle for a given triangle.† It is not enough to say that we want a pedal triangle for a given triangle; we will also need a special point that goes with the pedal triangle, which is called the pedal point.† Letís start with a triangle ABC and a pedal point P.
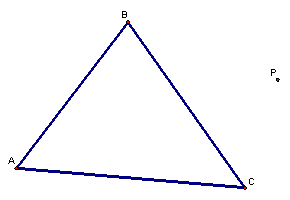
We first create lines along the sides of the triangle.
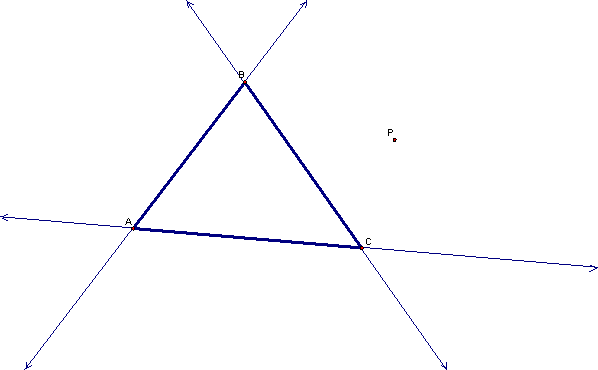
Then we construct perpendicular lines through the point P to each of the lines of the triangle.
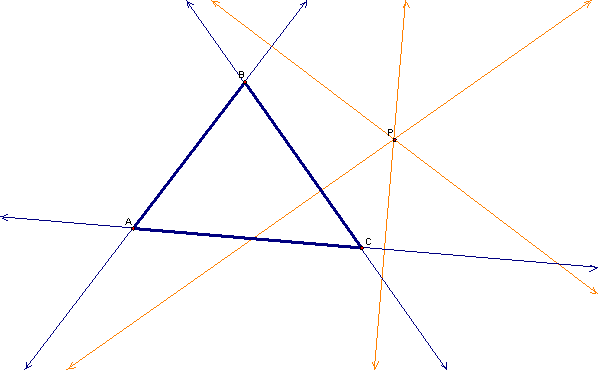
Next, we find the intersections of the perpendicular lines and the lines of the triangle ABC, and we call these points R, S, and T.
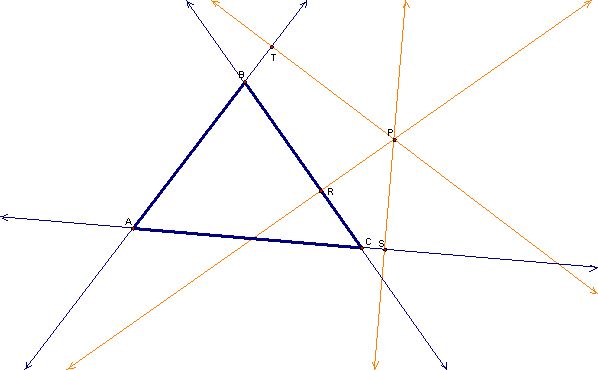
The triangle formed by RST is the pedal triangle for triangle ABC and point P.
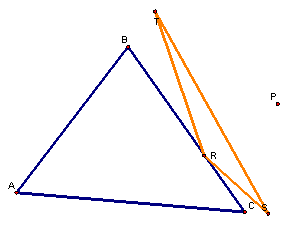
If we hide the construction lines, we can see the picture a little clearer.† We have
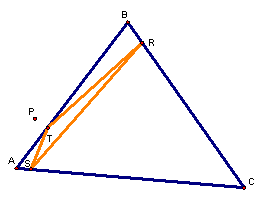
If we move the point P, we can see that the pedal triangle is very dependent on the relative location of P to the triangle ABC.

So by definition, the pedal triangle is the triangle formed by connecting the intersections of the perpendiculars from the point P to the sides of the triangle ABC.† Experiment with the location of the pedal triangle using GSP by clicking here.
The Simson Line
There is a unique situation that can be spotted while you move around the point P.† See if you can find a location for P where the pedal triangle reduces to a line segment.† One such point is show below.
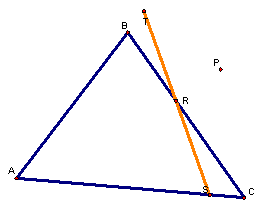
It is not a unique point, even though it is a unique situation.† To prove this, letís construct the circumcircle of triangle ABC.† This looks like
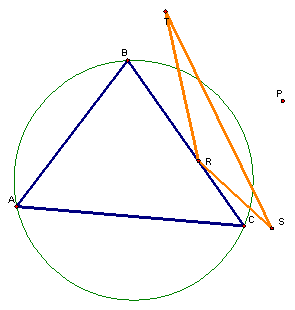
Next, letís use GSP to merge the pedal point to the circumcircle.
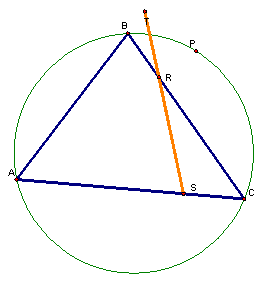
Again, we see that the pedal triangle is reduced to a line segment.† This special line is called the Simson Line.† We can rotate P around the circle and see some of the different Simson Lines.† Click here to see the animation.

Special Cases of
the Simson Line
As the point P is rotated around the circumcircle, there are three special cases.† Each of these cases is when the side of the triangle is also the Simson Line.† Letís look at those three cases.
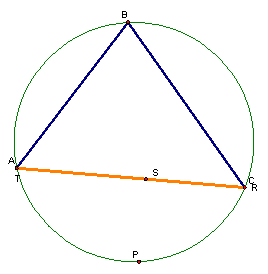
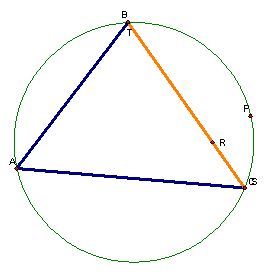

Is there something unique about these points on the circumcircle?† Why do the pedal triangles at these points reduce to the side of the triangle?† We will have to construct some more lines to investigate this.
First, letís show the perpendiculars through point P again.
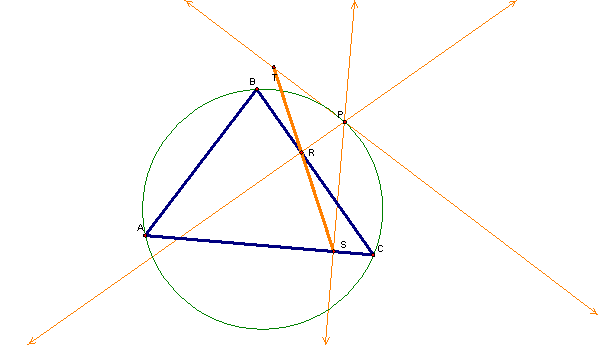
If we then rotate the point P around to a point on the circumcircle such that the point is the intersection of the perpendiculars through two of the vertices of the triangle (for example A and B), we get
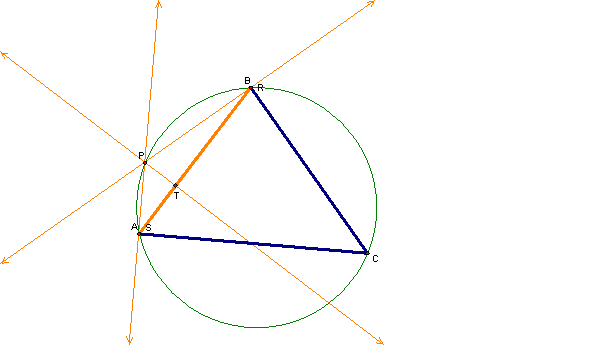
We see that the angle PAC is a right angle, and that the angle PBC is also a right angle.† Finally, we see that the pedal triangle (and the Simson Line) is the side AB. †Therefore, to get the point that makes a Simson Line that is the side of the triangle, simply construct the perpendicular lines through the vertices and the intersections of those lines are the pedal points that yield the unique Simson Lines.

Conclusions and
Extensions
The pedal triangle is a unique triangle that is defined by a given triangle and another point on the plane.† These pedal triangles have many different properties, and we have barely started to describe them in this discussion.† The Simson Line is even a more unique situation, in that if the point P in on the circumcircle of the triangle, the pedal triangle is reduced to a line segment.
Some other things that could be investigated with pedal triangles are the relationship between the pedal triangle and other special triangles of the given triangle, for example if the point P is one of the unique centers like the centroid.† Also, one could investigate the locus of the midpoints of the sides of the pedal triangle as the point P rotates around a circle on the plane.