
EE6680 Assignment 1
Exploring the Distance Formula and Lemniscates
By Kevin Perry
The Distance Formula
Let us first consider a point in the Cartesian coordinate system, (a,b). The distance from the a point (x,y) to this point is
![]()
For all of our demonstrations, let’s pick two specific points, (3,4) and (-5,-2). Their distances from the origin are
![]()
![]()
We can now explore how these two equations can be manipulated to create geometric shapes.
Circles
If we first set the distances D1 and D2 to a fixed constant, we can find all the points in the coordinate system that are equidistant from the individual points. We see that set of points that now satisfies the equations are circles with their centers at (3,4) and (-5,-2).
![]()
![]()
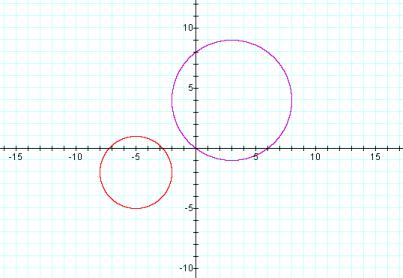
The circles are centered at the points, and the radius of each circle is equal to the constant value of the distance D.
We can re-arrange the equation by squaring both sides. For the first point we have
![]()
or
![]()
If we then substitute back in for the generic point and change D to r (standing for radius) we have
![]()
which is the familiar formula for a circle centered at (a,b) with a radius of r.
Ellipses
Next, let’s take the two distances D1 and D2 and sum them together and set that equal to a constant. The equation would be
![]()
This equation describes the set of points in the coordinate system that when taking the sum of their distances from the two points maintains a constant. The value of C must first be examined.
The first thing that is important with C is the distance between the two points. It can be inferred that the sum of two distances from a single point to the two fixed points cannot ever be less than the distance between the two points. Therefore the value of C cannot be less than the distance between the two points. To get the distance between the two points, use the distance formula using (3,4) for (x,y) and (-5,-2) for (a,b). You get
![]()
![]()
![]()
![]()
![]()
So the constant C must be greater than or equal to 10.
For the graph of the equation at C=10, the set of (x,y) that satisfy the equation is merely a line between the two points (3,4) and (-5,-2), which can be easily verified.
For values of C greater than 10, for example a C value of 13, the equation and graph is
![]()
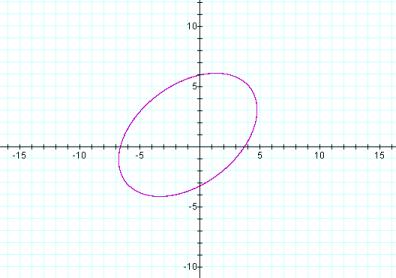
This figure is elliptical in shape, and appears to contain the two points. For various values of C we get the following graphs.
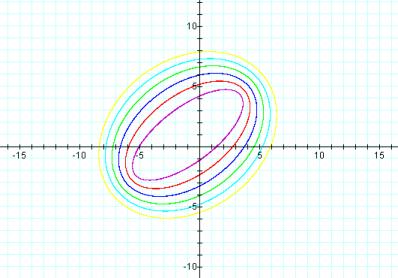
As can be seen from the graph, the sets of points are always an ellipse, and always contain the two original points.
If we create a generic equation
![]()
we can say that this equation describes an ellipse around the foci (a,b) and (c,d) with a “radius” of R.
Other shapes
Next, if we were now to take the product of the two distances and set it equal to a constant we would have
![]()
This describes a set of points whose distance from the two foci have a constant product. There is now no limit on the constant C other than it must be positive. It must be positive because the two distances are positive (by definition) and the product is therefore positive.
For the equation where C=0, the graph is merely the two points, because the only way to get a product of zero is to have one of the terms be zero. This can only be accomplished by having (x,y) be one of the two foci.
But as C gets larger, the shape of the graph transforms, as can be seen in the following graph
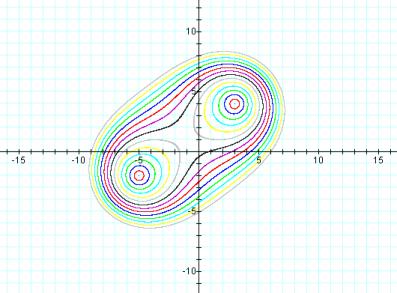
You can see from the graph that the sets of (x,y) start as small circular shapes centered at the foci, and then progress to teardrop shapes and peanut shapes until the set of points starts to describe a strange elliptical shape. Although these shapes (at higher values of C) look elliptical, they are not ellipses by the definition of an ellipse.
One may ask, what about the point where the graph changes from two separate shapes to one single shape. That point will be covered in the next section.
Lemniscates
For the product of the two distances that we explored above, there is a point when the graph of the set of points satisfying the equation changes from two sets of contiguous points to one set of contiguous points. For the equation above this happens when C=25, which is shown in the graph below.
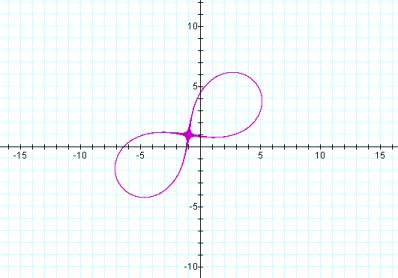
This figure 8 symbol is called a lemniscate. One would then ask why did this happen at C=25. How is 25 related to the distances? Earlier, we computed that the distance between the two foci was 10. If we take half the distance between the points and square it, we get 25. Therefore, the general formula for a lemniscate would be
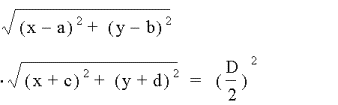
where D is the distance between (a,b) and (c,d).
If we were to limit the two foci to the x axis, and shift the points such that they are centered on the origin, then the points could be represented (a,0) and (-a,0). Therefore the general equation for the lemniscate becomes.
![]()
For a value of a=4 we get a graph that looks like
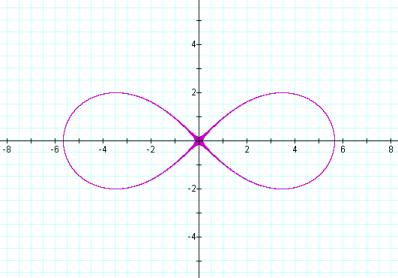
The lemniscate formula can also be manipulated to simplify it.
If we square both sides of the equation, we get
![]()
By multiplying out the left side, we get
![]()
and simplifying
![]()
then factoring
![]()
This equation is the simplified equation for the lemniscate discussed above. If we graph this equation for various values of a we get.
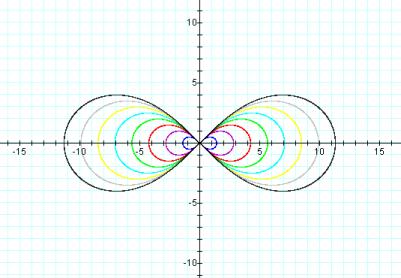
If we add a constant value to the lemniscate equation, we can further change the graph
![]()
so for a=5 and b=10 we get
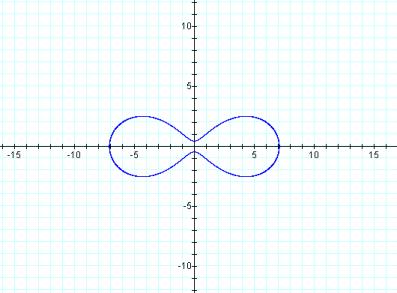
Finally, we want to translate the lemniscate equation into polar coordinates. Starting with
![]()
To transform into polar coordinates, we substitute
![]()
![]()
Therefore you get
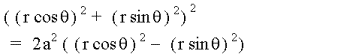
which is
![]()
and simplified is
![]()
where the trigonometric function can be whatever simplified form you prefer.
Conclusions and Extensions
We have seen that the simple distance formula between two points can create a multitude of geometric formulas and also create some interesting new shapes. The extension to this discussion would be to find other forms with two distance formulas to see if they made sense, for example division and imbedded functions.