
EMAT6680 Final Assignment
Triangle Segments
By Kevin Perry
Problem Set-up
In this discussion we will investigate the segments of a triangle created by choosing an arbitrary point P on the plane that contains a triangle ABC, and then making line segments from each vertex through the point P. So the figure would look like
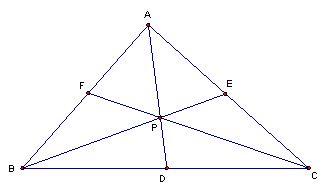
The point P does not necessarily have to lie within the triangle, so that the figure could also look like
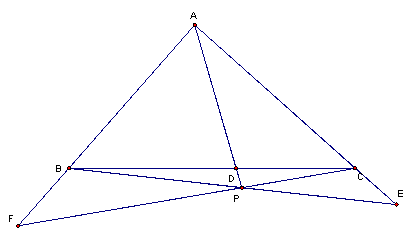
Segments of the
Triangle
With this construction, we have created line segments AF, BF, BD, CD, CE, and AE around the perimeter of the triangle.† If we take the length of the segments for a particular P we get
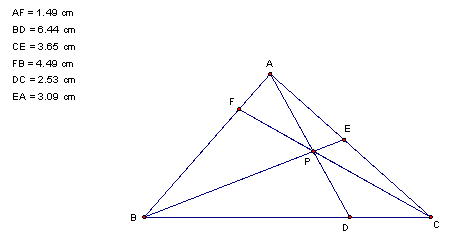
These do not look all that interesting all by themselves, but if we take some products they might be more unique.† For example, letís take the products of the segments starting at each vertex and going counterclockwise around the perimeter.
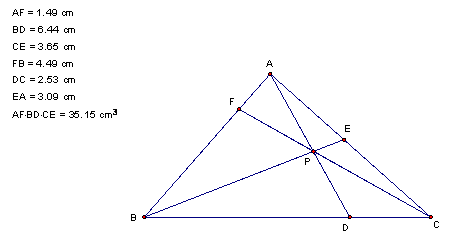
Next, letís take the product of the segments starting at each vertex and going clockwise around the perimeter.
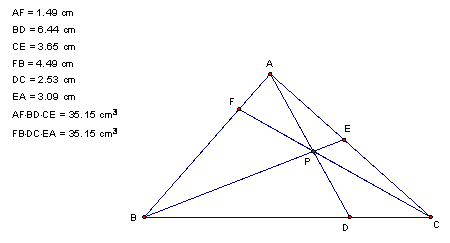
And now notice that the two products are equal!† In this case, both products are 35.15.† If we choose another point for P, we get
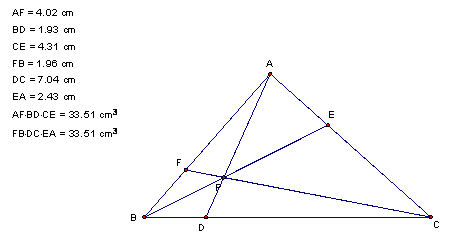
What if P is not inside the triangle?† The figure would look like
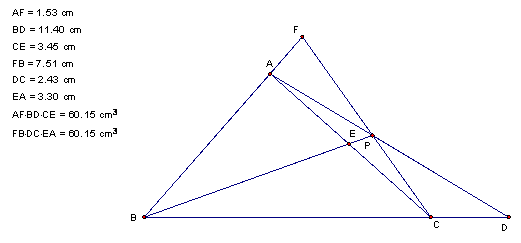
Amazingly, the product is still the same.† Check this out for yourself in this GSP file.
This fact begs for a proof.
Proof of the
Product of the Segments
The first step in proving these products are the same is to construct parallel lines at each vertex to the two cross segments from the other vertexes.† In other words, at vertex A, we construct a parallel line to BE and CF, and then we do the same for the other two vertices.† The result looks like

Then, we want to extend the interior segments in both directions to create lines.

Then, we need to label some of the points of intersection to create similar triangles.
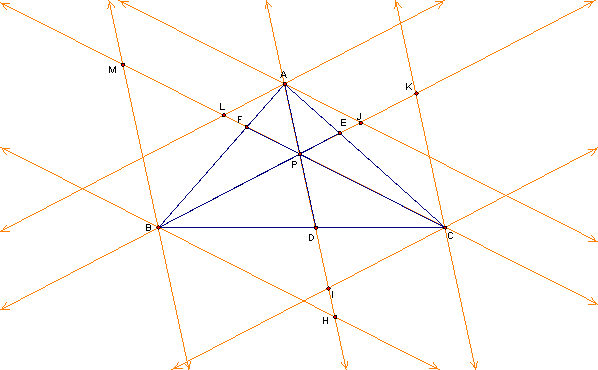
First notice that AFL is similar to BFP and AFP is similar to BFM.† There are also similar triangles at each vertex.† From these similar triangles, we get

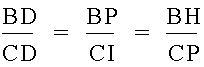
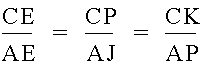
Next, we note that CPD is similar to CMB and also that BPD is similar to BKC.† From these triangles, we get
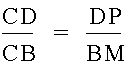
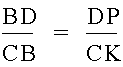
If we manipulate these two equations to get another ratio of BD to CD, we can get
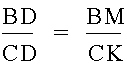
If we look at the other similar triangles at each vertex, we get two more ratios
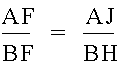
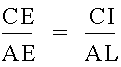
Now, we are ready for the proof.† We want to prove that
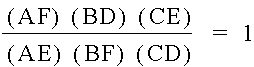
We can manipulate the equation into
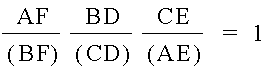
Now, if we choose wisely from the above equalities that we have brought out from the similar triangles, we can see something interesting.† There are many solutions from this point, but we will pick one.† First, note that
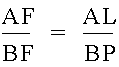
which is from the first set of equations.† Next, note that
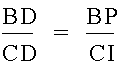
which is also from the first set of equations.† And finally note that
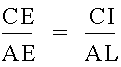
So, if we substitute all of these into our original equation, we have
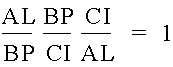
And we can cancel out the terms and see that
![]()
Therefore, the ratio of the products is always 1.
The best thing about this proof is that it really doesnít matter if the point P is inside or outside of the circle.† Check it out on the GSP file.
Area of the
internal triangle
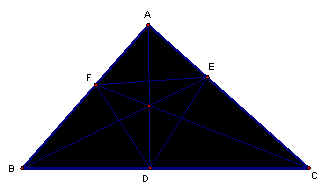
If we make a triangle out of the intersection points, then we have an internal triangle to the original triangle based upon the point P.† The picture would look like
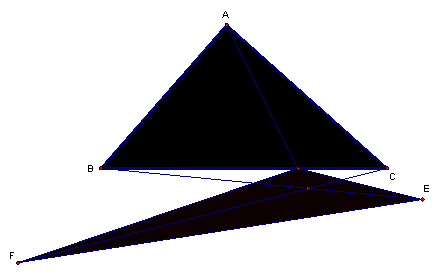
If P goes outside the triangle, there is still an ďinternalĒ triangle, for example
If we limit the point P to the inside of the triangle, we can investigate the area of the internal triangle compared to the area of the original triangle.
Letís first think intuitively about this area.† If the point approaches one of the sides of the triangle, the internal triangle gets very small, and the area approaches zero.† Therefore the ratio of the original triangle to the internal triangle approaches infinity.
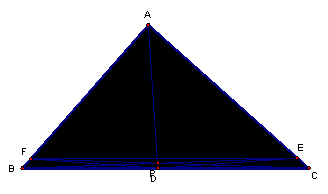
As the point P approaches the centroid of the triangle, the
internal triangle is the median triangle.
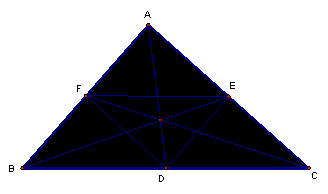
From our previous analysis, the ratio of the original triangle to the median triangle is 4.† This can be quickly confirmed by noting that the median triangle forms four similar triangles, and in fact four congruent triangles.† So the ratio is four triangles to one triangle, and therefore 4.
With a little more analysis, you can see that the median triangle is going to be the largest internal triangle that can be formed.† Therefore, the ratio of the areas is always greater than or equal to 4.
Use this GSP file to experiment for yourself.
Conclusions and
Extensions
We have shown that the segments created by choosing an arbitrary point on a plane with a triangle and drawing the intersections of the vertices and the point have a unique relationship.† Namely, that the ratio of a certain product is always one.† We have also seen that the ratio of the areas of the original triangle and the new triangle formed by the intersections is always greater than or equal to four.