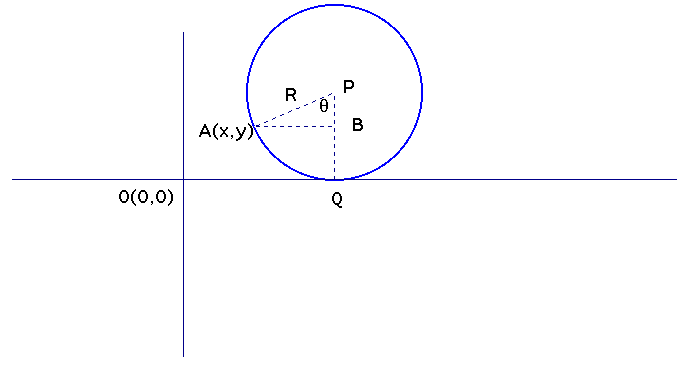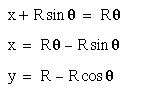PARAMETRIC EQUATION OF
A CYCLOID
(Venki Ramachandran)
PARAMETRIC EQUATION OF
A CYCLOID
(Venki Ramachandran)
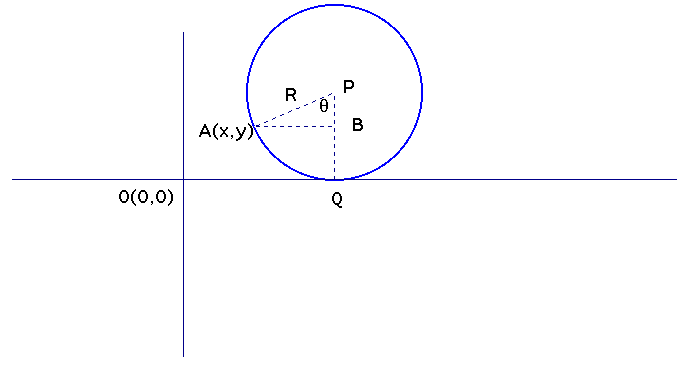
Suppose we start with
a circle with center P. Let A be a point on the circumference.
At time t=0, let the point A be on the origin O (0,0). At time
t, the circle would have moved forward such that, the co-ordinates
of A are (x,y) and the co-ordinates of B are (m,n).
Now in time t, the point
A would have described a distance = R theta along the circumference.
This is also the horizontal distance moved by the center of the
circle P.
This horizontal distance
moved by the center will be from Origin to the point Q = x + AB
= 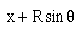 This gives us
This gives us 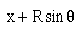
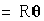 or
or 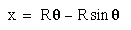 Considering the Vertical
distance, Y = PQ-PB =
Considering the Vertical
distance, Y = PQ-PB = 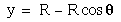 Thus we have
Thus we have
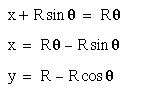 We also know that the
circle would be moving with a constant angular velocity, W. Where
theta = Wt.
Thus the equations can
be represented as
x = R Wt - R Sin (Wt)
We also know that the
circle would be moving with a constant angular velocity, W. Where
theta = Wt.
Thus the equations can
be represented as
x = R Wt - R Sin (Wt)
y = R - R Cos(Wt)

Return to my
web page