

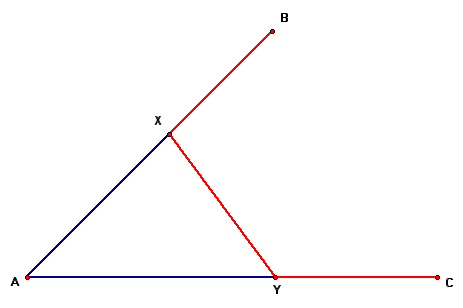
The challenge is to find two points X and Y on AB and AC respectively such that BX = XY = YC. At first it would seem simple and with a little bit of playing around, it does turn out to be indeed so.
Take a look at the figure below and see if you can do it before scrolling down to see my solution. Does your solution match mine? I would be delighted to read your's if its different from mine.
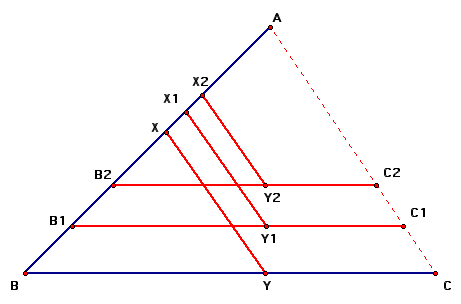
One of the first things I realised was that obviously the points X and Y are unique. BUT, if we maintain the angle BAC constant but draw parallel lines to AC intersecting AB at different places, there would be different points X and Y. However, there would be some relationsip between the family of X and Ys
Thus, I believe that as shown in the figure below, there would be angles ABC, AB1C1, AB2C2 etc and points X1 Y1, X2 Y2 and so on that could be drawn to satisfy our requirement.
I believe that Y, Y1 and Y2 will be in a straight line because the angles formed at B, B1 etc are equal as are the angles formed at C,C1 etc.
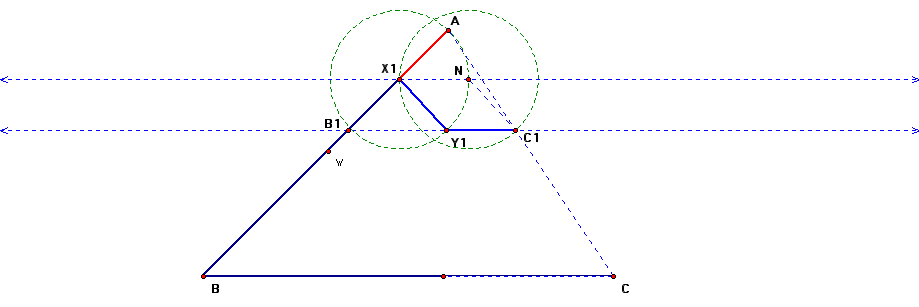
What I have done above is to randomly select a point X1 on AB. Then I joined AC and drew a line through X1 parallel to BC. Now comes the crucial part. I need to find a point C1, that lies on AC, such that the line drawn through C1, parallel to BC, will contain a point Y1 that is equidistant from C1 and X1 and be equal to AX1.
To do this, I first draw a circle with X1 as center and radius AX1. This circle intersects the line through X1 and parallel to BC at N. With N as center and the radius once again equal to AX1, I draw a second circle. This intersects AC at C1. A line through C1, drawn parallel to BC will intersect the circle drawn with X1 as center. I label this point Y1. Now, AX1 = XN = NC1=X1Y1=Y1C1. I have thus solved our problem, had we started with angle AB1C1.
The next step is to join AY and extend it till it meets BC. Let this point be Y
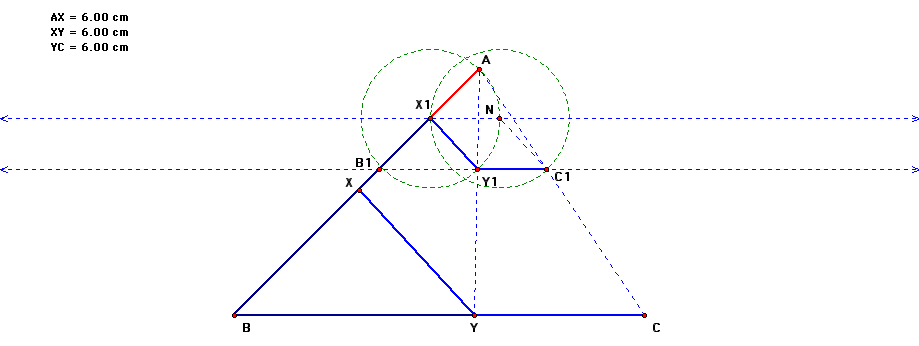
Finally, I drew a line through Y, parallel to X1Y1. This line intersects AB at X. Upon measuring, it is noticed that AX = XY = YC, just what we set out to do.