

Given a triangle ABC, we can of coure construct a triangle whose vertices are random points on the sides of triangle ABC. The question is, which of those triangles would have a minimum perimeter.
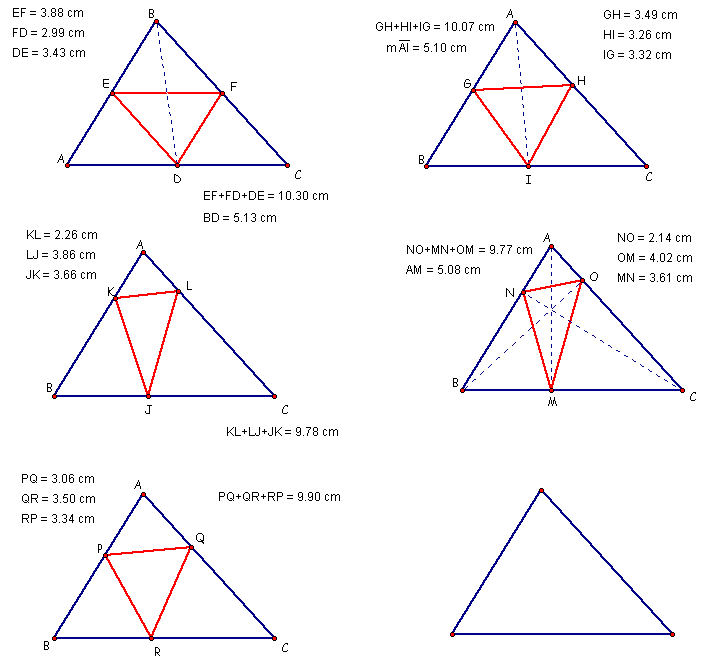
I began by constructing triangles from recognized points on the sides AB, BC and AC. For example, I took the mid points of the three sides and constructed a triangle by joining these points. I next took the circumcenter of the triangle and dropped perpendiculars to the sides and constructed a triangle using the point of intersection. Another triangle that I considered is one drawn from the point of itntersection of the altitudes dropped from the vertices to the opposite side. Finally, I also tested a triangle constructed by joining the perpendiculars dropped from the incenter of the triangle.
I found that the triangle constructed using the point of intersection of the ALTITUDES has the minimal PERIMETER.
