

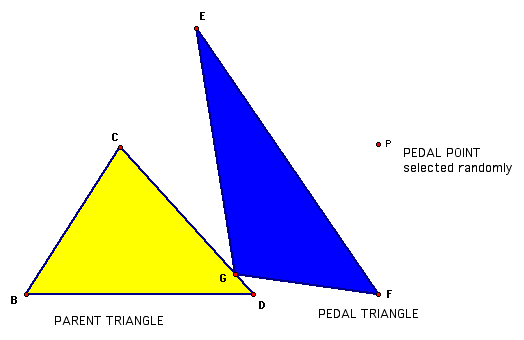
We are going to construct the PEDAL triangle of triangle BCD. A point P is chosen randomly to be the PEDAL point. This point can be inside or outside triangle BCD. From P, we drop perpendiculars to the three sides BC, CD and BD. We may have to extend the sides beyond the perimeter in order for the perpendicular to intersect the sides. We then join the three points of intersection of the perpendicular and sides. This triangle (EFG in our example) is the PEDAL triangle. We notice that moving P simply changes the shape of the PEDAL triangle. In fact, when P is inside triangle BCD, the PEDAL triangle also moves within BCD.