

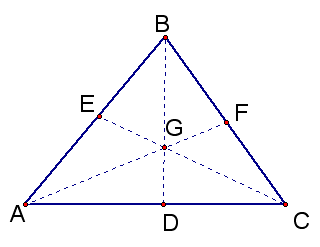
The Proof that I came up with, after trying a variety of approaches is given below:
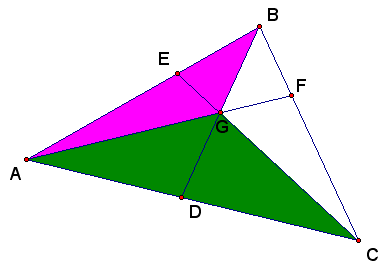

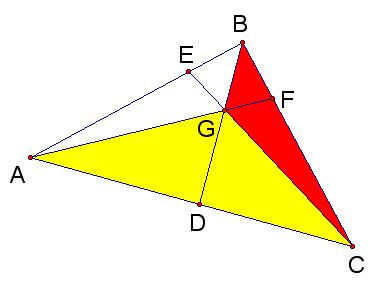

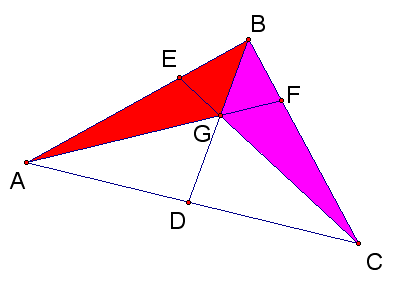

Having found the ratio of the segments and the ratio of the areas of the shaded portion in each of the three cases, we are ready for the final assault!

PROOF ! PROOF ! How does the area of the shaded portions relate to the segments as I seem to have so nonchalantly assumed. The proof is given below!
Consider the triangle and the shaded area shown below:
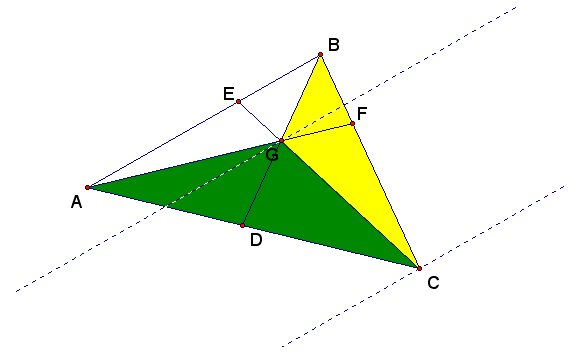
For convenience, I have drawn two lines parallel to AB, one passing through G and another through C.

