

Here we show that the distance between the CENTROID, CIRCUMCENTER and the ORTHOCENTER of any triangle always maintain a constant ratio. HG = 2 G C
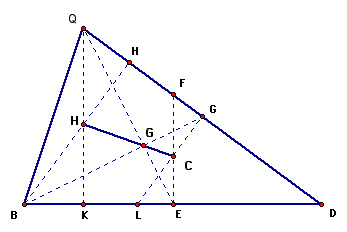
We construct the three centers of the triangle first. The Orthocenter is the point of intersection of the perpendiculars BH and CK. The circumcenter is the point of intersection of EF and GL. These two lines are the perpendicular bisectors of the sides CD and BD. The Centroid is the point of intersection of BG and CE. These are the lines drawn from the vertex to the midpoint of the sides opposite to the vertex.
We now need to prove that the length HG is twice the length of GC.
Consider the two triangles HCG and CAE. These two triangles are similar. Proof of this similarity is easily recognized by observing that lines FE and CK are parallel. Thus angle ECG = angle H. Further, angle CGA = angle HGC being vertically opposite angles.
Therefore, CG : GH as QG : GE.
We know that G being the CENTROID of the triangle divides QE in the ration of 2:3. Thus, QG:GE = 1:2.
Therefore, CG : GH as 1 : 2.