Lemniscate
By: Ginger Rhodes
Lemniscate
Consider
the two points (3,4) and (-5,-2).
For any point (x,y) we can write the distance equations for these as
Distance 1 = 
Distance 2 = 
Now, lets look
at these at the graphs of these equations if the distances are equal to 2.
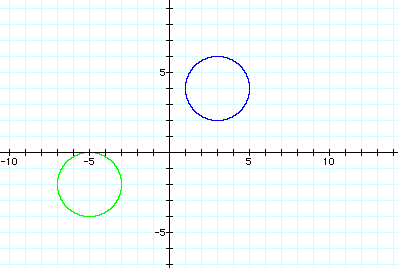
Notice circles with radius 2 are graphed. The center of the blue circle is (3,4)
and the center of the green circle is (-5,-2).
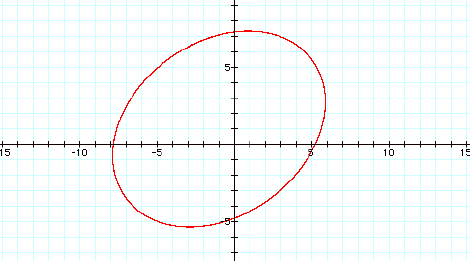
Suppose we look at the sum of these equations.
Lets look at the graph of the sum when it equals 15.
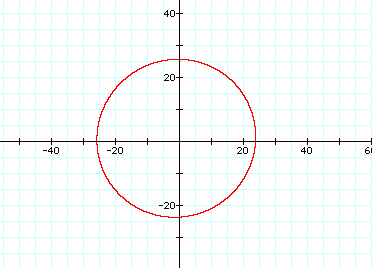
Now, lets look at the sum when it equals 50.
Lets consider the product of the
distance equations.
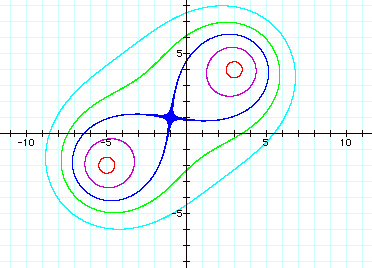
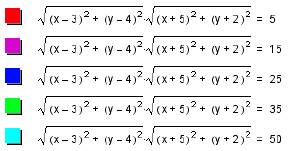
To look at an animation of the product of distances
equations click here.
If the
two given points are (-a,0) and (a,0) then the lemniscate has its center at the
origin (0,0) and major axis along the x-axis. For example, let a=0.
Then
will be this lemniscate:
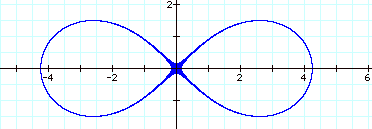
Now, we can simplify the
equation.
So the equation 
can be simplified to 
.
In general, if the foci of the lemniscate are (-a,0) and
(a,0) then the equation in Cartesian coordinates is 
.
Lets look at a couple of
examples:
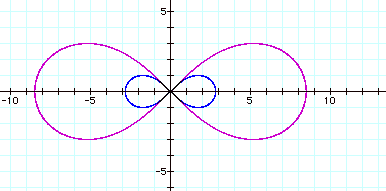
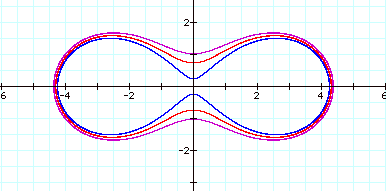
Suppose we now look at the equation 
.
Lets try different values of b for
when a is 3.
Now we will translate 
into an equation
in polar coordinates.
Remember 
and 
, where 
.
Therefore,
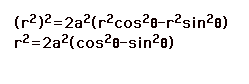
So 
for 
.
