A Cycloid

By: Ginger Rhodes

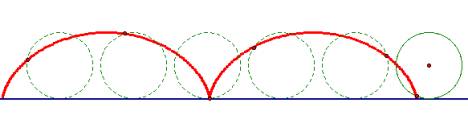
A cycloid is the locus of a point on a circle that rolls along a line. Click HERE to see a GSP animation showing the cycloid.

Let’s explore the cycloid. First, find the parametric equation for the cycloid. Remember a parametric curve in the plane is a pair of functions

x = f ( t )

y = g ( t )

where the two continuous functions define ordered pairs (x, y). The two equations are called the parametric equations of a curve. The extent of the curve will depend on the range of t.

To do this I will look at part of the curve.

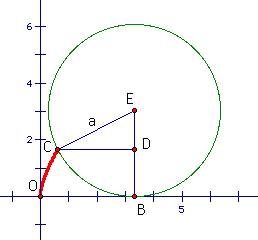
Now, we need to find the coordinates of point C.

X-Coordinate: To find the x-coordinate we will find the length OB and subtract the length CD. OB is the same as arc CB, which is (t/2p)·2pa or at, where t is the radian measure of the angle BEC. Using trigonometry we find CD = a sin t.

So, x = at - a sin t or x = a ( t - sin t ).

Y- Coordinate: To find the y-coordinate we will find the length BE and subtract the length DE. BE is the length of the radius, a. Using trigonometry DE = a cos t.

So, y = a – a cos t or y = a ( 1 – cos t ).

Let’s take a look at the graph using Graphing Calculator 3.1:

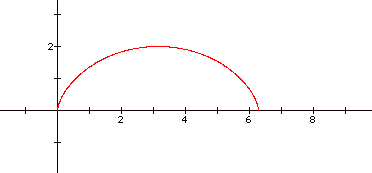
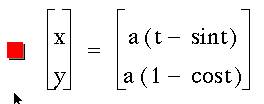
For values a = 1 and values of 0 £ t £ 2p.

Now, what happens as the variable a varies? Click HERE to see the animation in Graphing Calculator 3.1.

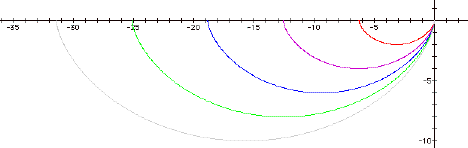
Let’s take a look at 1 £ a £ 5

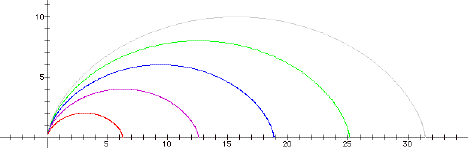
red graph: a = 1, notice the x-intercepts are 0 and 2 p

purple graph: a = 2, the x- intercepts are 0 and 2·2p

blue graph: a = 3, the x- intercepts are 0 and 3·2p

green graph: a = 4, the x- intercepts are 0 and 4·2p

grey graph: a = 5, the x- intercepts are 0 and 5·2p

What happens when the variable a is negative? Let’s take a look at –5 £ a £ -1.

RETURN