
Tangent Circles
By: Ginger Rhodes
Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point of tangency begin the designated point.
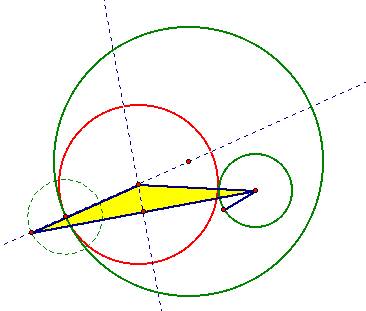
Notice, I constructed an isosceles triangle.
The center of the desired circle is the intersection of the perpendicular line to the base of the isosceles triangle and the line through the center of the circle.
Click HERE for a script tool to create these tangent circles.
Do you notice anything interesting about these circles?
Why not trace the center of the tangent circle as the
point of tangency moves along the circle—click HERE.
What did you see?
Do you know how you could justify your conjecture?
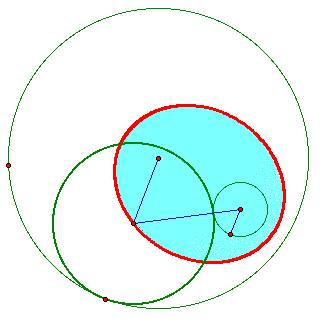
Notice, the sum of the lengths from the center of the original circle to the center of the tangent circle to the center of the other given circle is constant. This sum is a constant, and therefore the locus of the centers of the tangent circles is an ellipse with foci at the centers of the given circles.
Question: Can you think of another tangent circle to the two given circles?
Click HERE for a script tool.
What do you think the trace of the center of the tangent circle looks like?
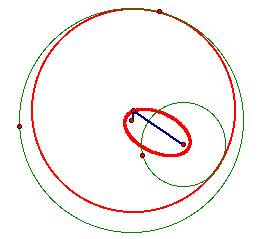
Wow- it’s still an ellipse! Now what do you think happens when one circle is not inside of the other—maybe on the circle?
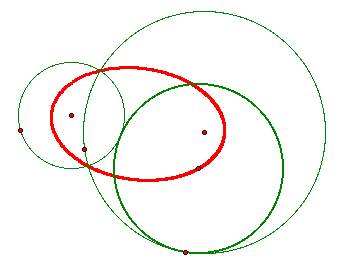
Again, it is an ellipse!
What if the smaller circle is in the exterior?
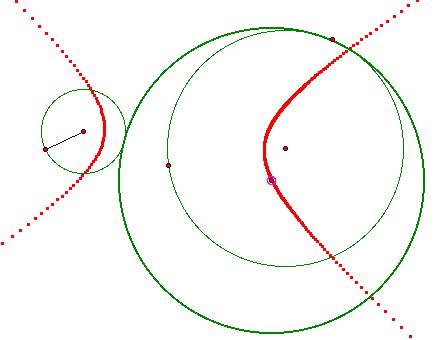
This looks like a hyperbola!
Click HERE to see an animation that shows the difference of the distances from the centers of the original triangle to the center of t he tangent circle are constant.