
Orthocenters
By: Ginger
Rhodes
Given: Triangle ABC. Construct the Orthocenter
H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C
respectfully.
Prove:
![]()
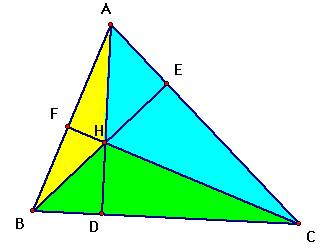
First, I want to look at
some examples to see if the
sum of the ratios does equal 1 and 2 for some specific examples. Click HERE for a
GSP file to explore.
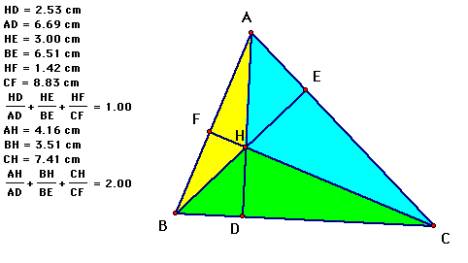
Ok- I now have specific
examples, but I need to prove it.
Part 1: I will begin with
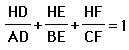
Notice the denominators are
the altitudes of the triangle ABC. If you multiply the altitude by the base and
1/2 you get the area of the triangle. So we will begin by multiplying each
altitude by the corresponding base.
![]()
![]()
Now, each
denominator is twice the area of triangle ABC. The numerators are the areas of
the respective smaller triangles HBC, AHC, and AHB.
![]()
Since the
denominators are the same I will add the numerators.
![]()
The three triangles in the
numerator of the fraction will add up to the area of triangle ABC.
![]()
Which equals 1
Therefore,
![]()
Part 2: I will now take a
look at the second part of the problem.
![]()
In part 1 I looked at areas
to establish the ratios added up to 1. It would be nice if we could use the
same type of reasoning to establish part 2. We have to think about how we could
get the numerator in terms of altitudes, so we can find the areas of the
triangles. Notice the numerators are part of the altitudes of triangle ABC;
therefore we will re-write the numerators by subtracting part of the altitude
from the entire altitude.
So AH = AD – HD, BH =
BE – HE, and CH = CF – HF.
From there we will use the
same reasoning as before and multiply each ratio by the length of the side that
will give the area of the triangle.
![]()
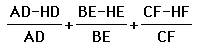
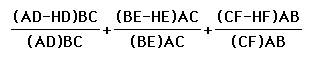
The denominators are twice
the area of triangle ABC. Notice, I am distributing in the numerator.
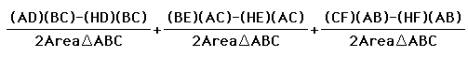
Notice the two lengths
multiplied together in the numerators result in twice the area of triangle ABC.
![]()
The two lengths left in the
numerators are twice the area of the smaller triangles. So,
![]()
Next, I simplify.
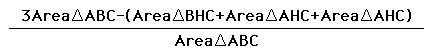
The triangles in the
parenthesis add up to the area of triangle ABC.
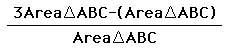
Simplify
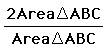
![]()
Therefore,
![]()