Polar Equations

By: Ginger Rhodes

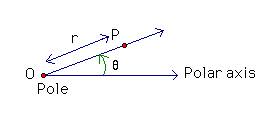
What are polar equations? A point P in a polar coordinate system is the ordered pair (r, q), where r is the distance from the pole to the point and q is the angle formed by the by the polar axis and a ray from the pole through the point. So (r, q) is called the polar coordinates of the point.

An equation whose variables are polar coordinates is called a polar equation.

These polar equations can create some interesting graphs. Let’s investigate!

Since (r, q) is the ordered pair for polar coordinates, I will begin by exploring some fundamental polar equations. For example, what do the equations r = 2 and q = p/4 look like?

r = 2 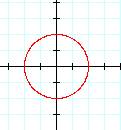q = p/4

These make sense because r = 2 represents a circle with radius 2 and q = p/4 represents a line that makes an angle of p/4 or 45° with the polar axis.

Now, I will look at the more interesting polar equations.

For example, what does r = a + b cos (kq) and r = a + b sin (kq) look like, when a = b = k = 1?

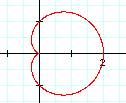
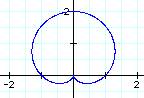
r = a + b cos (kq) r = a + b sin (kq)

It’s a limacon!

Notice both equations have the same shape and size, but are rotations of each other. For this reason I will only explore properties of

r = a +b sin (kq).

What happens if the values of a and b change, but k still equals 1?

There are two possible cases.

CASE 1: 0 < a < b

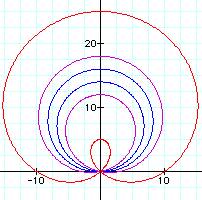
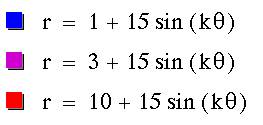
What happened? It looks like there is an inner loop, and the loop gets smaller as a approaches b.

CASE 2: 0 < b < a

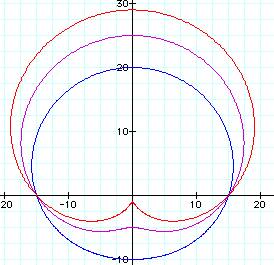
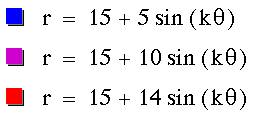
There is no inner loop and as b approaches a it appears to be a circle.

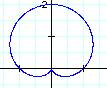
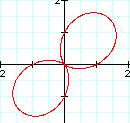
Next, I will investigate what happens as k varies. Let a = b = 1.

Looks like a Lemniscate!

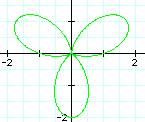
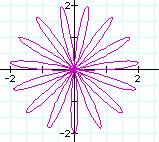
It’s starting to look like a flower! Any conjectures? It seems the k value represents the number of leafs in the n-leaf rose. What do you think the value of k is in the following graph? Click HERE for the answer.

What is the relationship between the graphs of r = a + b sin (kq) and r = b sin (kq)? I will begin by letting a = b = k = 1.

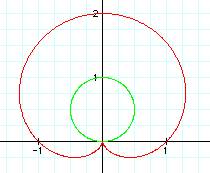
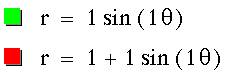
It looks like the green graph is a circle. What happens when k changes?

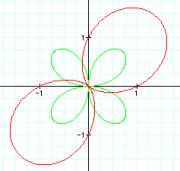
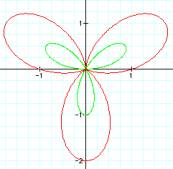
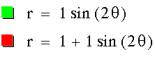
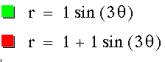
Any conjectures? Here are some more examples:

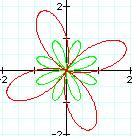
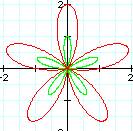
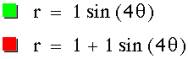
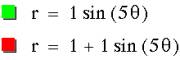
When the polar equation is r = sin (kq) it appears there are k petals when k is odd and 2k petals when k is even. In comparison r = 1 + sin (kq) there seems to always be k petals. When k is odd the petals of r = sin (kq) are inside of r = 1+sin (kq). See to more petals form click HERE.

What happens for 0 < k < 1? Click HERE for an animation.

RETURN