Proof of the Multiplication

of the Ratios Equal 1

By: Ginger Rhodes

Given: Triangle ABC, Point P in the interior of triangle ABC with AP, BP, and CP extended to their intersections with the opposite sides at D, E, and F respectively

Prove:

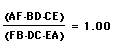
Proof: Draw an auxiliary line through the point A and parallel to segment BC. Next, extent segments CF and BE until they intersect the parallel line and label those points H and G, respectively.

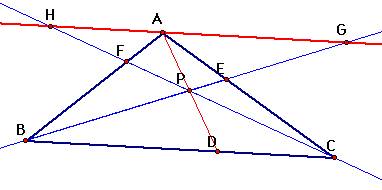
Now, the following triangles are similar by Angle-Angle Similarity because in each case one pair of angles are vertical angles (therefore congruent) and the other pair are alternate interior angles formed with parallel lines (therefore congruent).

Since similar triangles, there are proportional sides (notice the proportions are set up to have the sides needed for the prove statement).

Now, I will multiply all the ratios on the left together and all the ratios on the right together.

Simplify

Multiply both sides by GA/AH. Therefore,

RETURN