The
Pedal Triangle
By:
Ginger Rhodes
What is the Pedal Triangle
for a Pedal Point P?
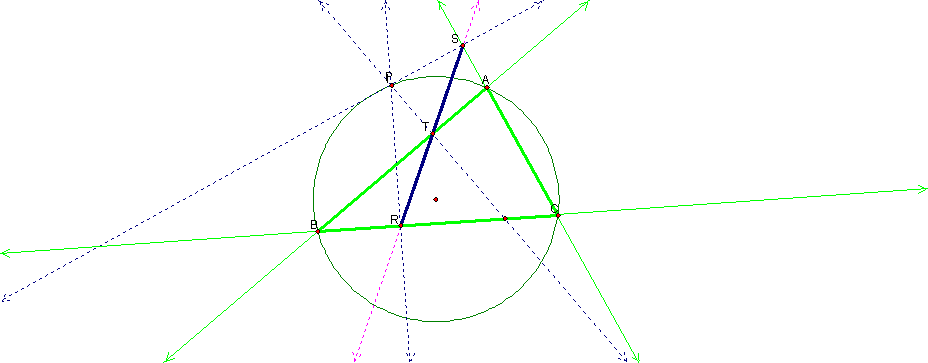
Construction of the Pedal Triangle: Begin with ∆ABC. If P is any point in the
plane, then the triangle formed by points of intersection of the perpendiculars
from point P to the sides of ABC is the Pedal Triangle.
Click HERE for a GSP file that allows you to explore
the Pedal Triangle and Pedal Point.
Did you discover anything
from your exploration?
First, I will discuss when
the Pedal point lies on a side of the ∆ABC. Click HERE for an animation of this
exploration.
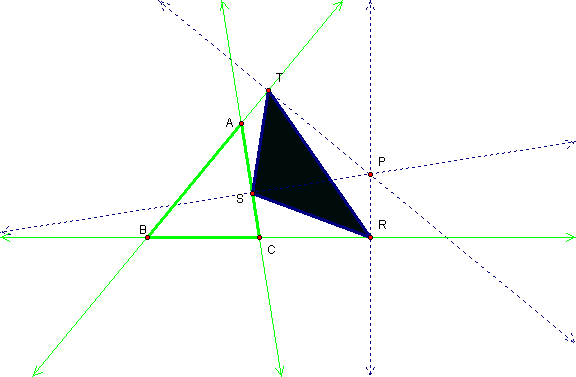
The Pedal Point P is on the
segment AC. Notice the Pedal triangle is inside of ∆ABC and the Pedal
point is a vertex of the Pedal triangle.
Now, does anything change at
the points A and C?
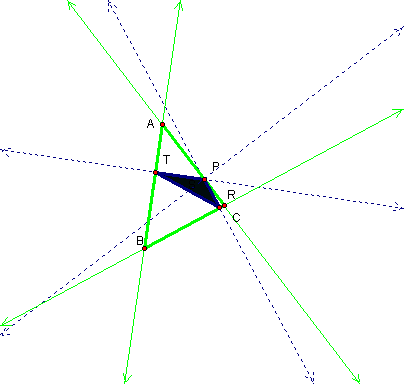
Yes, the points R, S, and T
are collinear. This line segment is called the Simpson Line.
What happens if ∆ABC is
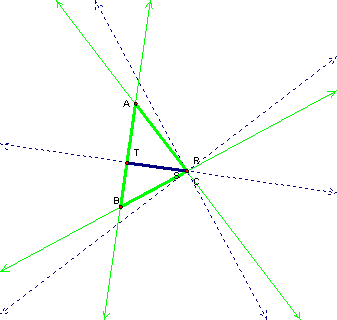
obtuse?
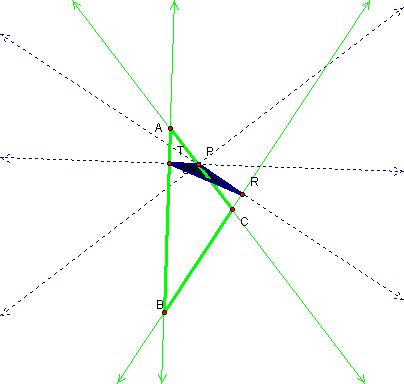
Part of the Pedal Triangle is
inside of triangle ABC and part of it is outside of triangle ABC.
Do you still get the Simpson
Line when the Pedal Point is on points A or C?
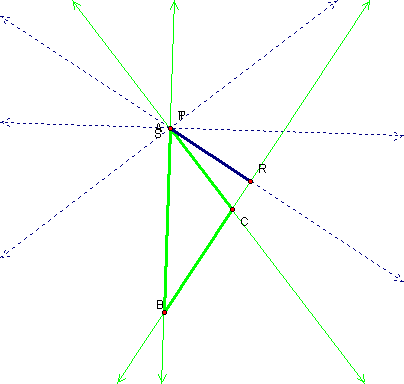
Yes, you do!
So, what are the conditions
in which the three vertices of the Pedal triangle are collinear?
It is the circumcircle of
triangle ABC. Click HERE for an
animation and HERE for a proof that R,
S, and T are collinear.
To find the envelope of the
Simpson line as the Pedal point moves along the circumcircle click HERE.
This is called the Deltoid
curve.