Thomas Earl Ricks

Assignment 1

The assignment for Assignment #1, number 6. is the following:

Graph:

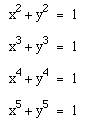
What do you expect of :

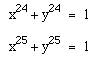
Upon graphing the following…

we obtain the following graph:

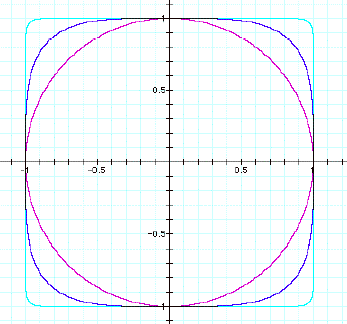
Upon observation, we would therefore expect the graph of:

to more closely approximate the unit square. We deduce this because the graph is even powered, as is the other two even powered graphs. As the power increases, we would expect it to look more and more like a unit square, as if a balloon were expanding in a unit box. Upon graphing, it does! (see below)

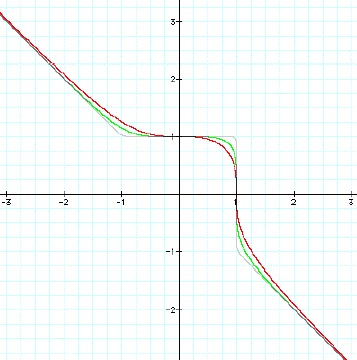
And upon observation of the odd powered graphs it appears that

would more approximate the function:

y = x

combined with the horizontal line at x=1 from -1<y<1

And upon graphing, it does!

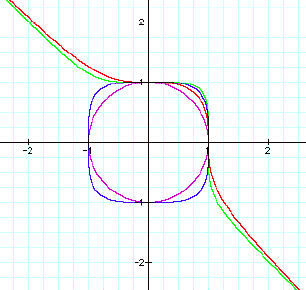
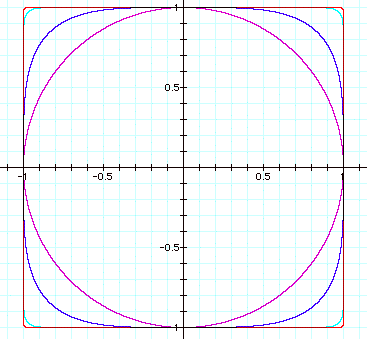
All the combined graphs look like the following:

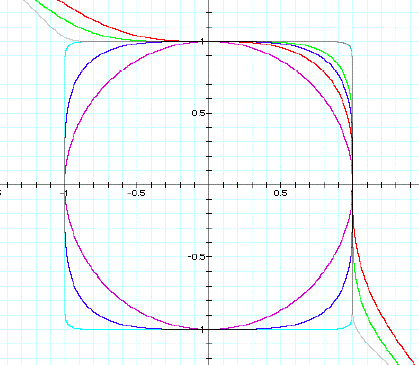
Another look at even powered graphs

From our observation of even powered graphs, it appears that we can form a conjecture that as the power increases, the graph more approximates the unit square.

If we graph:

we can see from this high-powered even example that it appears our conjecture may be correct:

The corners are what appear to be interesting areas. Let us zoom into the upper right corner:

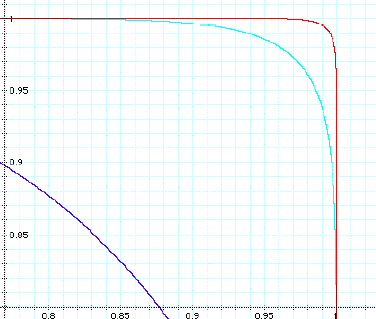
Now let us use the enormous power of the computer to graph

And we get:

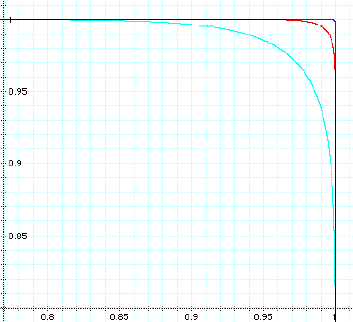
This new graph is a very close approximation to the unit square!

Just for fun, let us look at some 3d graphs of even and odd powers!

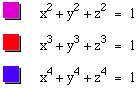
The blue graph is shown slightly transparent so the inner purple graph can be seen. We might conjecture from the two even graphs that the higher power the even power, the more the graph approaches the unit square!

That is left for you to explore!