Thomas Earl Ricks
Mathematics Education
Assignment # 10
“The Cycloid”
Assignment #10:
A cycloid is the locus of a
point on a circle that rolls along a line. Write parametric equations for the cycloid and graph
it. Consider also a GSP
construction of the cycloid.
First, we will consider constructing the cycloid on
GSP, and then we will attempt to create a parametric equation for the cycloid.
GSP Construction
We start by constructing the line that our circle will
roll on:

We now wish to construct the path our circle will
follow as it rolls on this line.
To do this, we construct a point A on the line with a perpendicular line
through A. This will serve as the
uniform height that our path will pass through. We then construct a circle with the radius of our
eventual rolling circle, to find a point for our path to pass through.
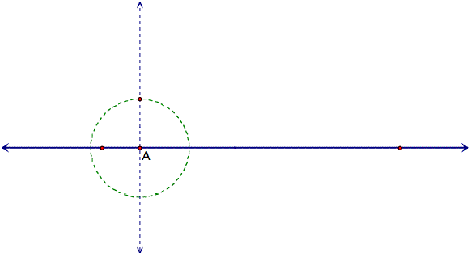
Now we construct the path through the upper
intersection point of the perpendicular line and the circle. Note that this path is parallel to our
original line. Our rolling circle
will follow this path. It is a
dotted red line in the diagram below:
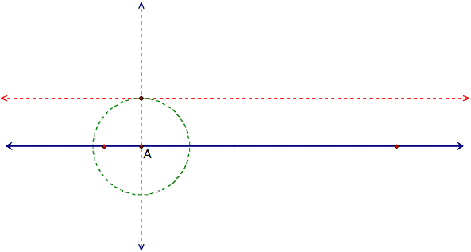
Now we place point C on the dotted red path, which
will be the center of our rolling circle, with a perpendicular line through
point C, so we can create a circle that has as its radius the distance between
the path and the original line. We
now construct rolling circle, the solid green circle pictured below, tangent to
the original line at point t:
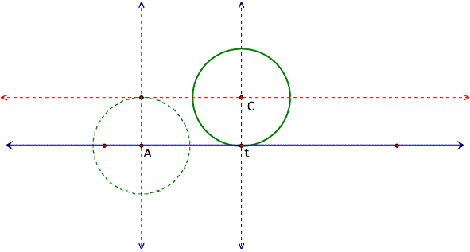
We can now hide everything but the original line and
our green circle with its center point C:
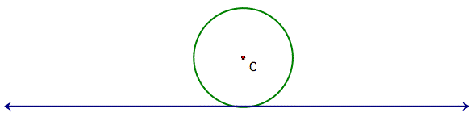
Let us add a spoke to show us the green circle
rolling, by creating a segment from point C to the green circle. And let us move our circle over to the
left, like so:

We now select the center point and our outer spoke
point, click on “Edit” in the Menu Bar, select “Action Buttons” and then
“Animate”. We wish for the circle
to move “backward”, which will move it to the right, so we select that, as well
as have our spoke point move in a “clock-wise” direction, so we adjust
that. We are now ready to animate
our rolling wheel. We select on
the outer spoke point, and select “Display” and then “Trace Point”. When we push the “Animate Points”
button on the screen, we should have our rolling circle roll to the right, with
the spoke turning, leaving a red trace of its path on the screen like so:
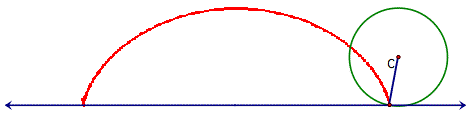
This is the locus of points created by a circle
rolling on path. It is actually just the beginning of
the locus, of course, the first hump of an infinite chain.
Hopefully you succeeded in creating one!
If we zoom out, we will see the cycloid path in more
detail, and observe that it is periodic, meaning it repeats itself over and
over. To zoom out, we could unhide
everything, resize our original dotted green circle to be smaller, and then
re-hide everything but the line, circle and spoke. Then when we animate, we obtain:
![]()
There are all sorts of fun ideas that can be pursued
from this idea of a circle rolling on a line.
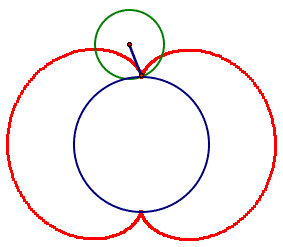
How about a circle rolling along a circle? What shape would that produce? Here is one if the green circle has a
diameter of half the blue.
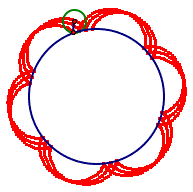
Here is one with less than one fourth diameter, after
several revolutions. What would it
look like if it kept going?
How about a circle rolling outside a triangle, or a
square, or a hexagon? Can you
think of any others and try them?
What about rolling inside these shapes?
Equation of a Cycloid
Now we will develop the equation of a cycloid. This is not an easy task and requires
some effort of thought. We can
look at our GSP trace to infer some ideas about what the parametric equation
will look like. 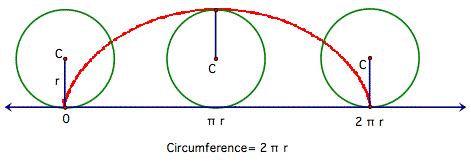
Since our rolling circle has radius r, and therefore
circumference ![]() ,
the circle makes one complete revolution as its center travels
,
the circle makes one complete revolution as its center travels ![]() .
.
Since the circle is rolling in time, let us say that
it takes ![]() seconds for the circle to complete one
complete revolution. By connecting
time to distance rolled, it will be easier to think about the situation.
seconds for the circle to complete one
complete revolution. By connecting
time to distance rolled, it will be easier to think about the situation.
So time is our independent variable, and we wish to
construct an equation that graphs the cycloid as a function of time t. We now need to observe the relative
position of the spoke point as time passes, both in the x and the y
directions. Let us look at the y
direction first as time passes:
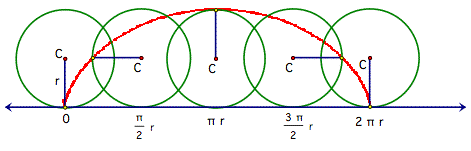
The spoke points are yellow to stand out from the red
path, and we have added the circle rolling in two more positions. Observe that at time 0, the height of
the spoke point is 0, while at
![]()
the height is 2r. Then the height falls back to r when time is at
![]()
and finally after one revolution, the height is back
to 0. This process repeats itself
with every revolution. The height also appears to be oscillating around the
height r. It begins below the line
y = r, and then passes through the line, and finally dips below the line again.
How could we describe the motion of the spoke point as
a function of t?
We observe that its motion is periodic with respect to
t, and that every ![]() units of time, it begins to repeat
itself. What functions do this?
Sine and cosine are obvious candidates.
units of time, it begins to repeat
itself. What functions do this?
Sine and cosine are obvious candidates.
Could we describe the height of the spoke point as a
function of t with sine or cosine?
Cosine would work, since if we combined it with the height r, we could
get it to oscillate back and forth around the line y = r, just as the spoke
point does.
We note that for time t = 0, cos(0) = 1. Thus we could find the height of the
spoke point using a function of cosine by taking the height r and subtracting
off of it rcos(0) = r. This would
reduce our spoke point height to 0.
Thus we have the equation y = r – r cos(t) as our equation.
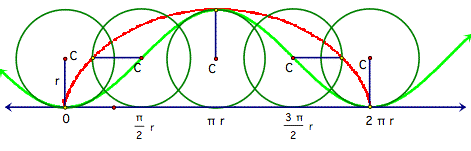
We observe that for the other values of t, this
equation accurately describes the height of the spoke point. We can see this more clearly by
observing the superimposed graph y=r-rcos(t) on our rolling cycloid.
Note that the yellow spoke point doesn’t follow the
light green cosine graph, but that the height of the spoke point follows the
light green cosine graph.
For example, at time t =
![]()
the cosine graph has height r, while the spoke does as
well.
We now need to create an equation for the horizontal
or x position of the cycloid, based on t.
We follow the same reasoning, but instead of looking at the height of
the spoke point at time t, we observe its horizontal position, relative to the
center of the rolling circle.
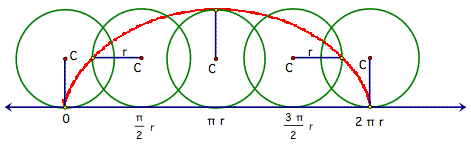
Observe that at time t = 0, the spoke point is also 0,
but as the center advances to
![]()
the spoke point is actually r behind! It then catches up to the spoke point
at
![]()
surpasses it at
![]()
and slows down to be at the
same horizontal position at ![]() .
.
What function of t could give this result?
A little playing reveals x = r t - r sin(t) matches
our values.
Thus our equations are:
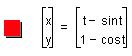
which yields the cycloid:
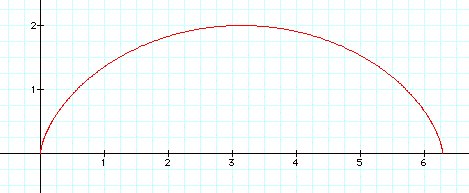
Or if we wish to zoom further out to see its periodic
behavior, we see:
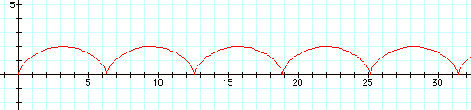
What other related equations can you discover?
Click here to
learn more about the Cycloid:
