Thomas Earl Ricks
Mathematics Education
Assignment # 12
“Fibonnaci Numbers and Ratios”
In this webpage we will explore the Fibonnaci
sequences and ratios.
To begin, the Fibonnaci sequence is the following:
1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , …
How do we get this sequence, you may ask?
Simple.
We begin with the first and second term being 1, and
then every successive term is the sum of the two previous terms.
The Fibonnaci numbers can be seen in a variety of
situations and in real life. Click here
to visit one such site.
Using Excel, we can create a quick spreadsheet that
shows the first 21 Fibonnaci numbers.
The column on the left, under “n” is the sequence number, and the
numbers on the right, under “f(n)” are the Fibonnaci numbers:
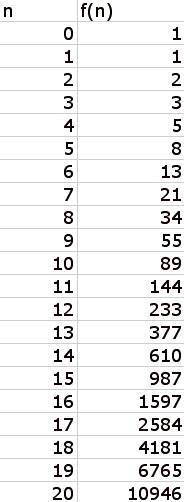
The Fibonnaci numbers grow quite rapidly!
We now wish to look at the ratio of consecutive
Fibonnaci numbers.
For example, the first ratio is the second Fibonnaci
number divided by the first:
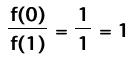
Continuing in this fashion, we will compute, using a
spreadsheet, each ratio of:
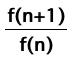
And we get the following for the first 27 Fibonnaci
numbers:
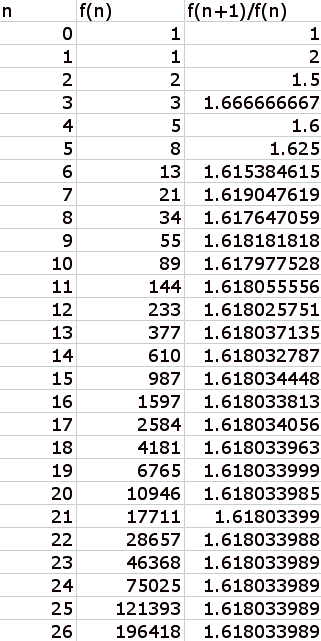
We notice that the ratio seems to approach
1.618033989.
We can have Excel draw us a graph of the ratios as it
oscillates back and forth to approach this number:
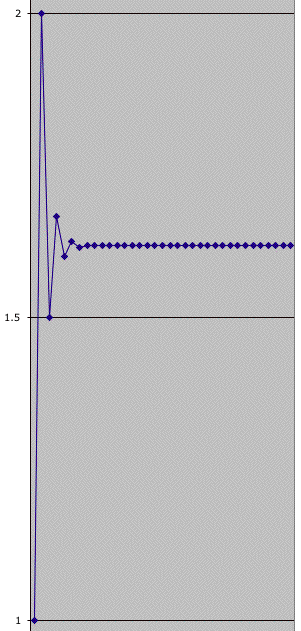
What is this number? None other than the golden ratio!
Click here
to learn more about the golden ratio.
An interesting thing is that the ratio of consecutive
terms is the golden ratio for other sequences similar to the Fibonnaci numbers.
For example, the Lucas sequence has f(0) = 1 and f(1)
= 3. Each succeeding term is the
sum of the two previous terms.
Thus, the Lucas sequence is constructed in exactly the same manner,
except that the two beginning numbers are different. The Lucas sequence is:
1 , 3 , 4 , 7 , 11 , 18 , 29 , 47 , 76 , 123 , 199 , …
The first 21 Lucas numbers are:
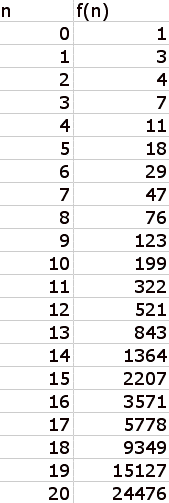
Now let us take a look at the ratio of successive
terms, just like we did with the Fibonnaci numbers. And guess what, the ratio is the same! On the right column is the ratio of :
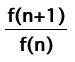
So here it is for the first 26 terms:
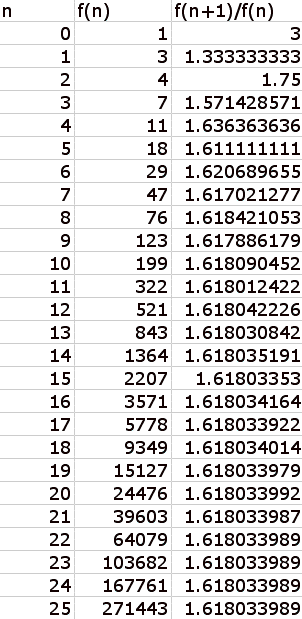
Thus we obtain the ratio as we did with the Fibonnaci
numbers.
But let us not stop there! We can also observe that if we make up our own sequences,
such as, oh, what should we do,…?
Let us have f(0) = 9 and f(1) = 25. Then each succeeding term is the sum of the terms
before. Then our new sequence is,
for the first 20 terms:
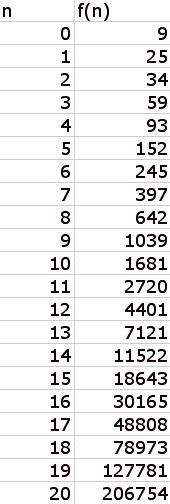
And when we take the ratio of succeeding terms, we
observe that we get the same ratio as with the Fibonnaci and Lucas sequence!
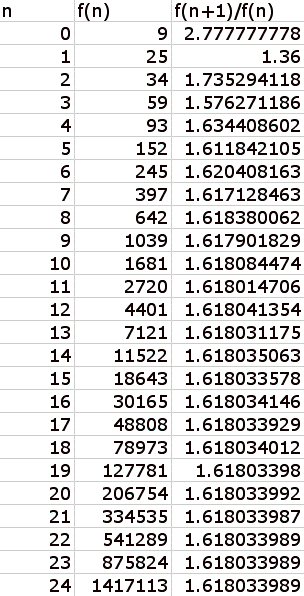
Pretty fascinating, isn’t it!
To find out why this is so, you can click here
to visit a website were it looks like a proof might exist to explain why the
ratio
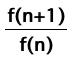
is equal to the golden ratio. (The explanation is talking about
Fibonnaci numbers, but I believe the proof will apply to any sequence with
similar form, like the Lucas sequence, where terms are the sum of the two terms
before.
Click here for
an Excel program where you can start your own sequence by choosing two numbers
that you like. This program also
shows that the ratio is the golden ratio!
