Thomas Earl Ricks
Mathematics Education
Assignment # 3
ÒRoots of a Quadratic EquationÓ
We will investigate in this webpage the roots of a
quadratic equation.
To begin, we start with the standard quadratic
equation, with a, b, and c as coefficients:
Drawing on our past knowledge, we remember the famed
quadratic formula, which allows us to find the roots of the quadratic
equation. The roots of the
quadratic equation are the solutions of the equation:
or in other words, the values of x which yield a y
value of zero. The quadratic
formula allows us to solve to find the two x values that make
true.
The quadratic formula is really two equations:
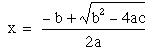
and
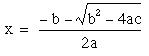
Solving these two equations will give the values of x
that ÒsatisfyÓ or make true the mathematical sentence:
It is really quite remarkable that just knowing the
coefficients a, b, and c, and then plugging them into the quadratic formula can
find the solutions!
There are actually a variety of alternative ways to
find the solutions of
by factoring (if possible), drawing the graph of
and observing where it has a height of zero (i.e.,
crosses the x-axis), trial and error guessing, etc.
The beauty of the quadratic formula is that it yields
the solutions EVERY time, with exactness.
We will now look at the quadratic formula in more
depth as it compares to the quadratic equation.
For simplicity, we will let a = 1 and c = 1. Thus the quadratic equation we will
look at is:
By setting this equation equal to zero:
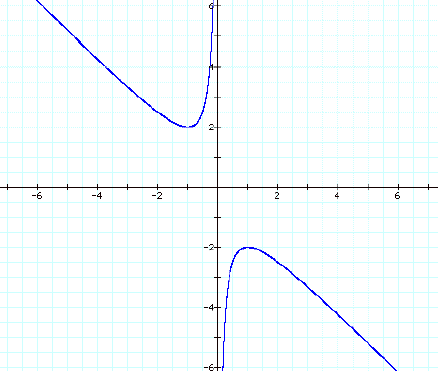
and graphing in the x-b plane, we obtain an unusual
picture:
What does this graph mean? How can we interpret this graph?
If we graph the line b = -2 then we get a horizontal
line that crosses the blue graph at one place, at x = 1. This means that for the equation
when b = -2 then x must equal 1.
And this is indeed true!
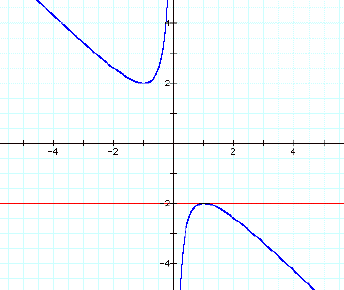
Therefore, the blue graph represents all the solutions
of the equation
for different values of b.
As another example, if b = 3, we observe that the line
b = 3 intersects the blue graph twice, somewhere around negative -2.6 and
Ð0.4. We graph the equation
in green and observe that indeed the green equation
does cross the x-axis at the precise x values for which the red line intersects
the blue graph! I have drawn
vertical purple lines at these two x values.
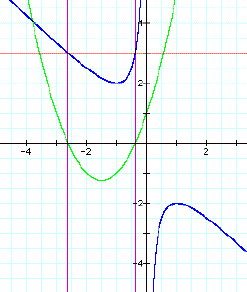
Now how do we connect this to the quadratic formula?
We observe that each of the two quadratic formulas can
be broken down into two pieces:
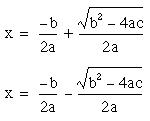
In the case of the quadratic equation
these two forms of the quadratic formula simplify to:
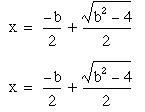
where b = 3.
In the graph below we draw the additional graph
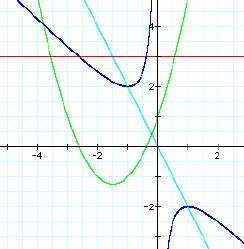
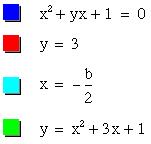
You may notice that the x value for where the light
blue line and the red line intersect is exactly half-way in between the roots
of the green quadratic equation (which means it is halfway in between where the
red line intersects the blue graph as well!)
What is going on here? What does this mean?
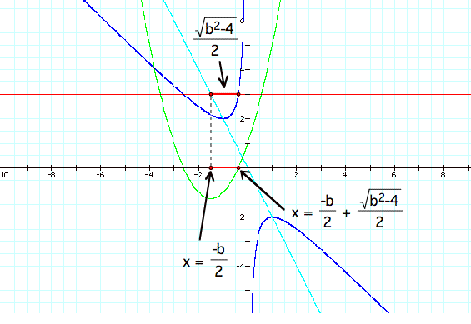The
x-value where the red and blue line intersect is the piece of the quadratic
formula
or since the red line is b = -3, then the x value is
which you can see on the x-axis. Since the place on the x-axis where the
green graph intersects is given by the quadratic formula
then we can see that distance from the x-value where
the red and blue graph intersect, which is
is given by
Adding these two pieces together gives us:
which is one of the roots of the green equation.
The second root is found by subtracting
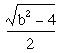
instead of adding it, which is the second quadratic
formula:
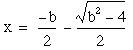
So instead of adding the thick red distance in the
graphic above, which distance was
we subtract that distance from
to find
the second root of the green graph, as shown in the graphic below by thick
purple lines:
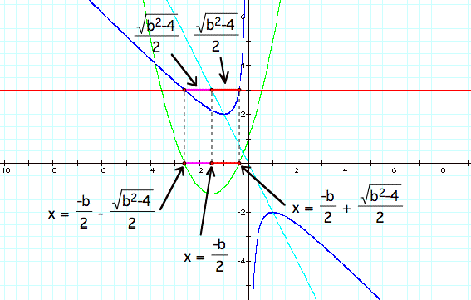
Thus by graphing
in the x - b plane, along with b = -3 and
we are able to find the roots of the original
quadratic equation
which is superimposed on the x - b plane to show where
its roots would be on the x-axis.
This is done by observing that we find the intersection of the line b =
-3 with
and add and subtract the distance
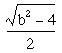
to find the solutions to
with b = -3, or the roots of
which is the same as looking at the two pieces of the
quadratic formula, which would give us the same result
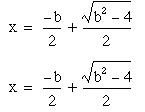
Or we could look at the intersection of the red and
blue lines to determine the roots of
I hope this has shed a little more light on the
quadratic formula!
Click here
for more information about the discriminant.