Thomas Earl Ricks
Mathematics Education
Assignment # 6
“Geometric Construction of a Parabola”
The Parabola
We are all fairly familiar with the quadratic equation
of the form:
![]()
This equation, when graphed, forms a parabola, such as
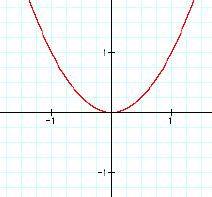
![]()
But there is also a geometric interpretation for a
parabola.
A parabola
is the set of points equidistant from a given line (called the directrix) and a given point not on the line (called the focus).
We will now go through a step-by-step construction of a
parabola using this definition by using Geometer’s Sketchpad.
GSP Construction of a Parabola
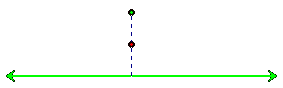
We start with a given line (the directrix) and a point
not on the line (the focus). We
will color both of these bright green for reference.

We now wish to find a way using GSP to identify all
the points that are equidistant from the line and focus point.
We could identify, for example, the most obvious point
equidistant from the line and focus, which lies halfway in between:
But how to find the others?
Remember, we want to find all the points that are the
same distance from focus as from the line, like so:
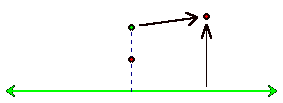
The distances (represented by the two black arrows)
should be the same.
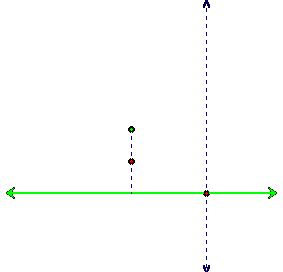
We may first notice that the distance from the line to
our point we are trying to find will always lie along the perpendicular through
the point to the line, like so:

But where should our point be? Just being on the perpendicular is not
enough. Where on the perpendicular
should our point lie so it is equidistant from focus to directrix?
We can solve this problem by relying on some
elementary geometric principles.
We first choose a point on our directrix for which our
perpendicular line will pass through:
We then construct a line segment from our focus to
this base point (we will also forget about the point below the focus for now,
so as to not confuse our diagram):
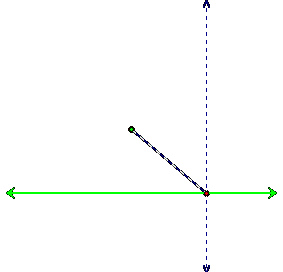
We then find the midpoint of this segment and draw a
perpendicular through it:
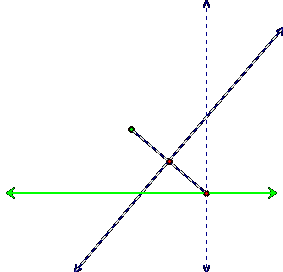
We mark the point of intersection of this
perpendicular with the other perpendicular, like so:
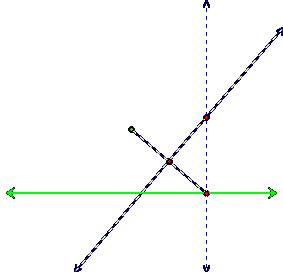
Does this intersection point look like it is
equidistant from the focus and the directrix?
Is it?
Can you prove it?
We will now provide a quick justification for why this
intersection point is equidistant from the directrix and focus.
Note that the line segment from the focus to the base
point of the perpendicular to the directrix is bisected, which means the thick
orange line segment is congruent to the thick purple line segment:
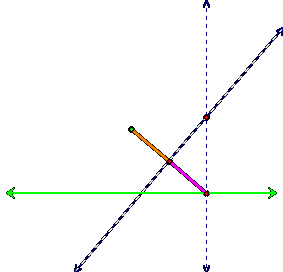
And the thick tan segment that is perpendicular to
these two segments is congruent to itself:
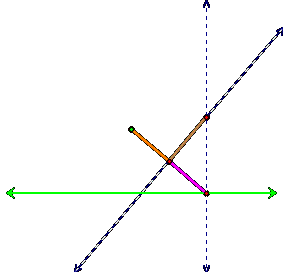
And the angle formed between the tan segment and the
orange is the same as the angle between the tan segment and the purple, since
the tan is perpendicular, which means both angles are ninety degrees
(represented by the thick grey right angle sign):
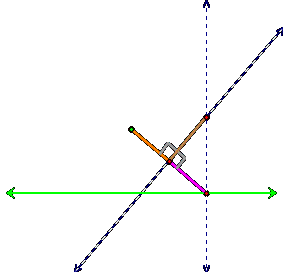
We therefore have two triangles that are congruent to
each other by the Side-Angle-Side theorem (SAS). Thus the orange triangle:
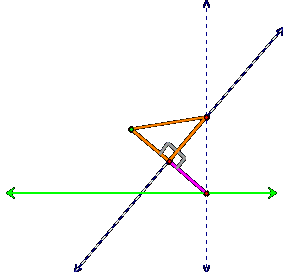
is congruent to the purple triangle:
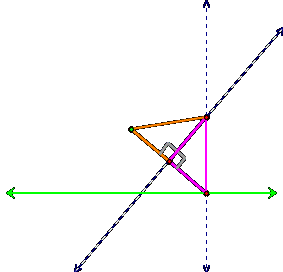
by the SAS theorem. This means that all corresponding parts of these congruent
triangles are the same. Therefore
the orange line segment from the focus to our intersection point is congruent
(or the same length) as the line segment from our base point on the directrix
to the intersection point:
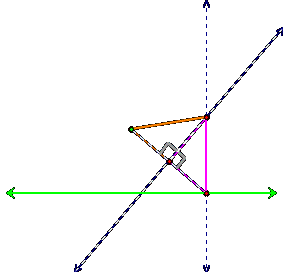
We have therefore developed a construction on GSP that
allows us to find a point equidistant from the directrix and the focus.
If we move our base point on the directrix, we can
find other points (light blue in the diagram below) that are equidistant, like
so:
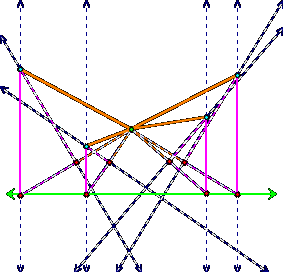
Therefore, we simply animate the base point on the
directrix in GSP, and trace the intersection point, to obtain a red trace of
the points equidistant from the focus to the directrix. This trace represents a parabola:
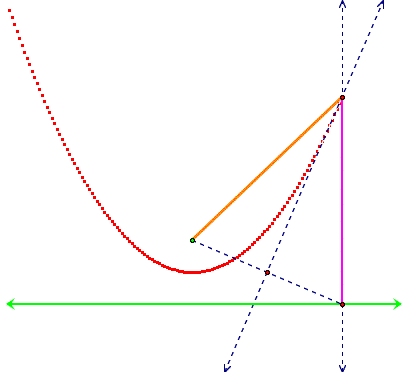
Now we can have all sorts of fun and experiment and
explore!
For example, what happens if the focus point is
brought closer to the directrix?
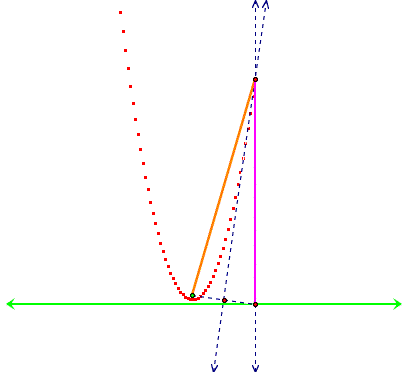
We get a steeper, or narrower parabola.
What if the directrix line is turned like so?
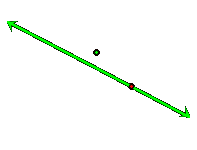
We get a parabola that is turned!
(By the way, running the animation for longer allows
more points to be shown on the trace.)
See if you can experiment and discover!
Have fun!
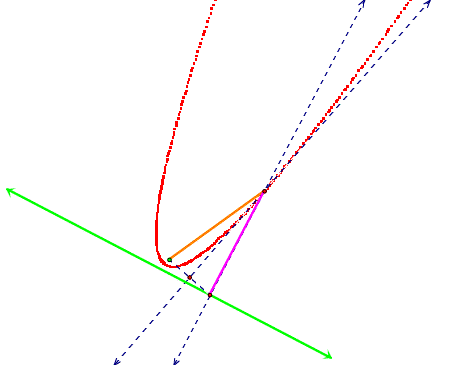
Here is a similar investigation using a circle as a
path instead of a directrix line.
With the focus inside the circle but not at the
center, we get an ellipse:
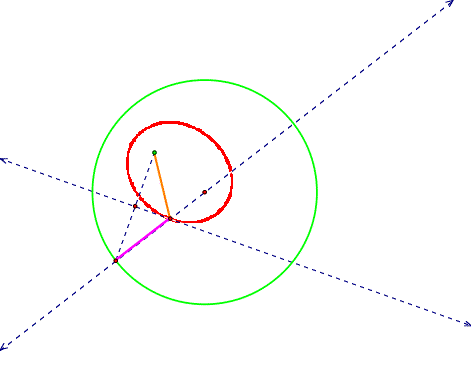
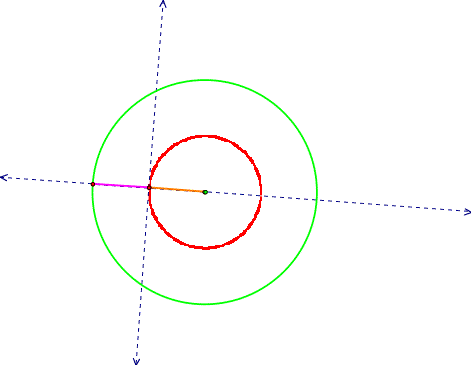
With the focus at the center we get a smaller circle:
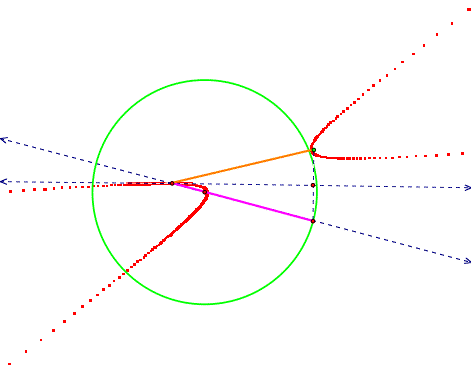
With the focus outside the circle, we get a hyperbola:
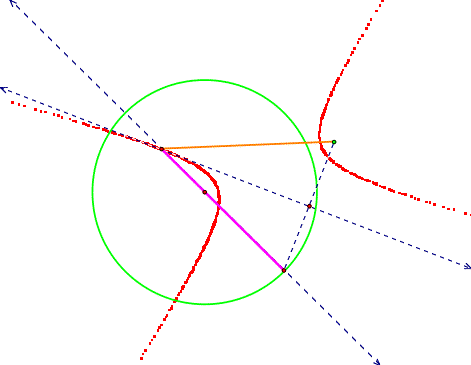
Notice the “steepness” of the hyperbola changes with
how close the focus is to the circle:
Click here for more information
about parabolas.
