Thomas Earl Ricks
Mathematics Education
Assignment # 7
“Tangent Circles”
In this webpage we will create tangent circles using
GSP.
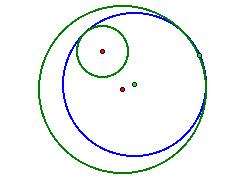
Our problem is as follows. Let us imagine that we have two circles, one inside the other,
and a selected point (light green) on the outside circle, like so:
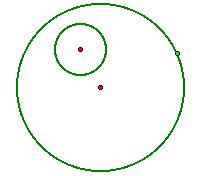
Our task is as follows. We wish to construct at this outside light green point a
blue circle that is tangent to both the outside circle and the inside circle,
theoretically like so:
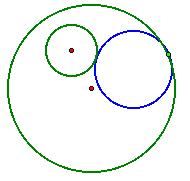
But we do not just want to guess where it is, but
construct it using geometric constructions.
We first observe theoretically that the outside circle
and the blue circle that is tangent to it at the light green point share the
same tangent line through the light green point:
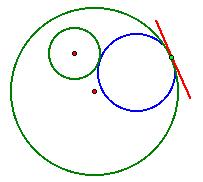
Running a perpendicular line to this tangent line at
the light green point will go through the outside green circle’s center:
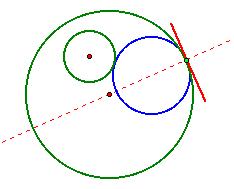
But it will also run through the blue circle’s
center! So we know that the blue
circle’s center lies on the line through the outside green circle’s center and
the light green point, so we construct that in GSP:
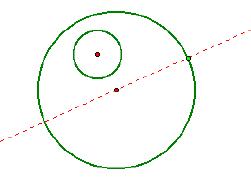
Now we return to our theoretical picture and observe
that the center of the blue circle, the center of the inside green circle, and the
point of tangency of the blue to the inside green circle all lie on the same
line as well.
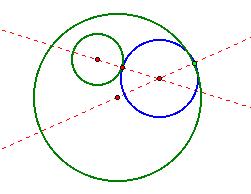
We are not so much interested in this line, as we are
in the observation that the distance from the center of the inside green circle
to the blue circle’s center is the radius of the inside green circle plus the
radius of the blue circle:
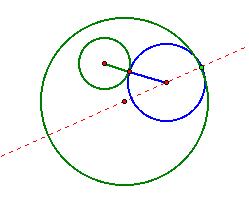
This observation is very important, for it allows a
way for us to pinpoint the center of the blue circle with exactness.
If we therefore construct a copy of the inside green
circle with its center at the light green point, we have a point, colored
purple in the picture below that lies the exact distance from the center of the
blue circle as the center of the inside circle does.

Observe that the purple point is one blue circle’s
radius plus one inside green circle’s radius distance away from the center of
the blue circle:
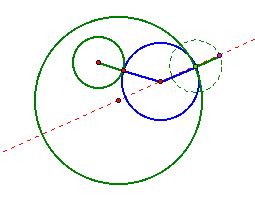
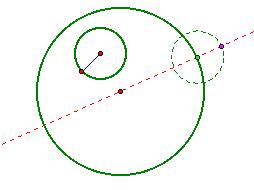
Therefore we construct this purple point on our GSP
construction by constructing a circle with the inside circle’s radius at the
light green point and finding the outside intersection of the dashed red line
with this new circle:
But now that we have this, how to find the exact
center of the blue circle? We know
its center lies on the dashed red line, but how to pinpoint it exactly?
To do this, we return to our theoretical picture, and
observe that the center of the blue circle lies at the apex of an inverted
isosceles triangle shown in red:
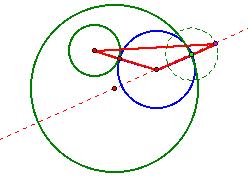
Since two of the sides are the same length, of length
radius of blue circle plus radius of inside green circle, this triangle is an
isosceles triangle. The base is
formed by connecting the center of the inside green circle with the purple
point.
Now we observe that the apex of an isosceles triangle
always lies on the perpendicular bisector of the base. Therefore, if we draw the perpendicular
bisector of the base (shown as tan-colored), the center of the blue circle will
lie on it:
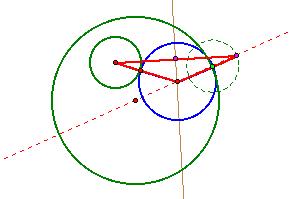
Therefore, the center of the blue circle lies on the
perpendicular bisector of the line segment connecting the center of the inside
green circle and the purple point.
But the center of the blue circle also lies on the dashed red line,
which runs through the center of the outside green circle and the light green
point.
So the center of the blue circle lies at the
intersection of these two lines!
Thus, returning to our GSP construction, we connect
the center of the inside green circle with the purple point:
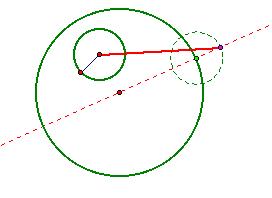
And draw its perpendicular bisector:
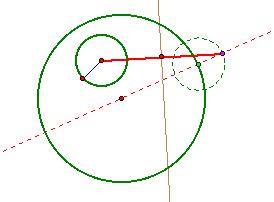
and then we identify the intersection of the perpendicular
bisector with the dashed red line:

This is the center of our blue circle, which we draw
with radius from the light blue point to the light green point:
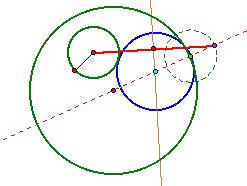
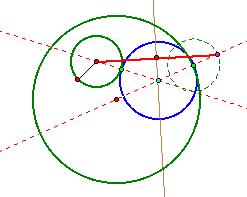
If we wished to identify the point of tangency with
the inside green circle, we could just draw a line connecting their centers,
and the tangent point (also colored light green) lies at the intersection with
the sides of the circles:
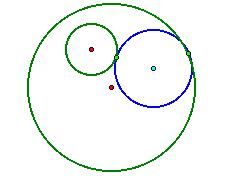
Hiding all the peripheral construction, we have our
final blue tangent circle properly constructed:
Further investigations:
Can you construct this type of tangent circle, that
encompasses the inside green circle?
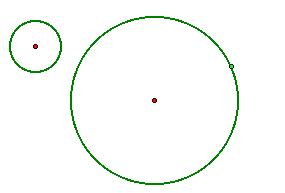
What if the green circles are separate? What type of tangent circles exist?
Click here for more
information on tangent circles.
