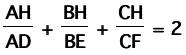Thomas Earl Ricks
Mathematics Education
Assignment # 8
Investigation 12
Orthocentric Ratios
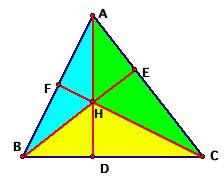
For investigation 12, we construct any triangle ABC,
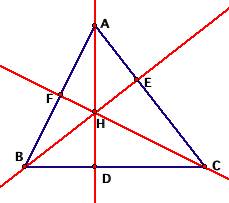
and then we construct the altitudes, creating points H
(the orthocenter) and D, E, and F, like so:
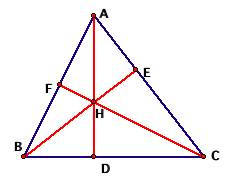
For ease of identification, we will only look at the
segments inside the triangle:
The first question is to prove:
![]()
To do this, we start with:
![]()
and multiply each part by a multiple of one, like so:
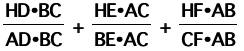
We then note that for each of the denominators, they
equal twice the area of triangle ABC:

since each denominator has an altitude of triangle ABC
and a base of triangle ABC. Thus
we can combine the three fractions with a common denominator like so:

and then we note that each piece on the top is twice a
certain triangle inside triangle ABC, namely:
![]()
![]()
![]()
This allows us to re-write the numerator in our
fraction to become:

and then after factoring out the common 2 on the
numerator, we get:

which 2 on the numerator reduces to one after division
with the 2 in the denominator, so we now get:

but then we notice that the three triangle areas on
the top are none other than the area of triangle ABC!
Therefore,
![]()
which allows us to combine the top numerator to just
the area of triangle ABC, which we also have in the denominator, so our
fraction equals 1:

Which means that our original ratio is 1:
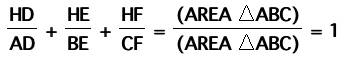
Which completes our proof! Therefore,
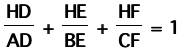
For the second part of investigation 12, we want to
show that for the same triangle ABC and constructed perpendiculars,
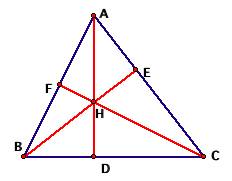
the ratio:
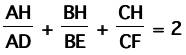
We start with
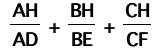
And want to show this equals 2.
To do this, we note that we can convert each numerator
in the expression above into an equivalent form, like so:
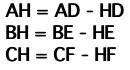
this allows us to make the substitutions:
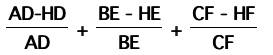
so that we can break each fraction up into two
fractions,
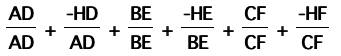
then we rearrange, like so:
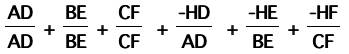
bringing out the negative sign from the last three
fractions:
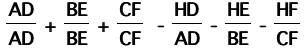
and then we factor out the negative sign from the last
three fractions:
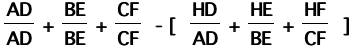
and then observe that the first three fractions are each
equal to 1:
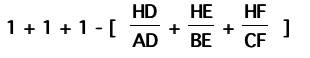
and then we remember in the first part of this webpage
that
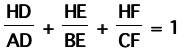
which allows us to make the substitution for the last
three fractions, obtaining:
![]()
which means we have proved: