ASSIGNMENT 1

Heather J. Robinson

EMAT 6680, Fall 2003

Linear functions can occur in one of two forms:

• Form #1: f(x) = k where k is a real number, or
• Form #2: f(x) = mx+b where m is not equal to 0.

In exploring operations of addition , multiplication , division , and composition with pairs of linear functions , f(x) and g(x), three cases can evolve from these two forms of linear functions.

• Case 1: f(x) = mx+b and g(x) = mx+b

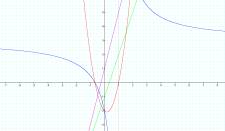
Let f(x) = 3x + 2 and g(x) = x - 1

f(x) + g(x) graphs a line with slope m_f + m_g and y intercept b_f+b_g.

f(x) ^. g(x) graphs a parabola.

f(x)/g(x) graphs a function with horizontal asymptote at 3/1 and vertical asymptote at x = 1.

f ^o g(x) graphs a line with a slope m_f*m_g and y intercept m_f * b_g + b_f.

• Case 2: f(x) = k and g(x) = z

Let f(x) = -2 and g(x) = 4

f(x) + g(x) graphs a horizontal line at k + z.

f(x) ^. g(x) graphs a horizontal line at k ^. z.

f(x)/g(x) graphs a horizontal line at k/z.

f ^o g(x) graphs a horizontal line at k.

• Case 3: f(x) = mx+b and g(x) = k

Let f(x) = 3x - 2 and g(x) = 4

f(x) + g(x) graphs a line with a slope m_f and y intercept at b_f +g.

f(x) ^. g(x) graphs a line with a slope g(m_f) and y intercept g(b_f).

f(x)/g(x) graphs a line with slope m_f/g and y intercept b_f/g.

f ^o g(x) graphs a horizontal line at m_f(g) + b.

---

Return to Ms. Robinson’s Page

---