Assignment 11
Investigation #1
Heather Robinson
EMAT 6680
Fall 2003
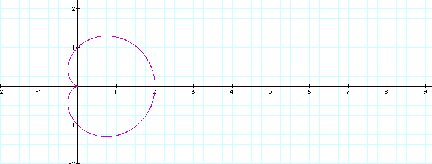
The graph of r = a + b cos kq is as suchÉ
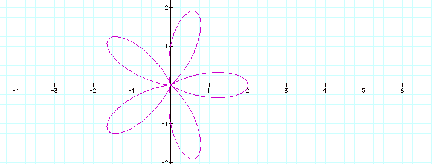
This graph can be elaborated to become the n-leaf rose. If a and b are fixed and equal, the n is completely determined by the value of k, if k is an integer. For example, the graph of r = 1 + 1 cos 5q looks like a flower (or rose) with 5 leaves.
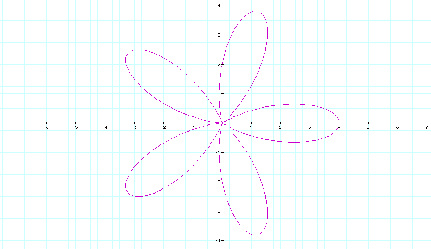
Further investigating a fixed value of k (in this instance, weÕll stick with 5) and maintaining a and b as equivalent shows that when a and b are equivalent, they dilate the image. The case below is when a = b = 2.
This is when a = b = -1.5. Changing the sign of a and b changes the orientation of the rose.

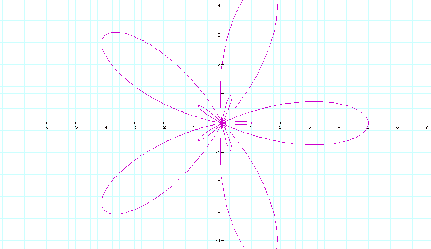
If a and b are different with a > b at this still fixed value of k, the rose begins to lose itÕs center. Here is the case when a = 3 and b = 2 while k still = 5.
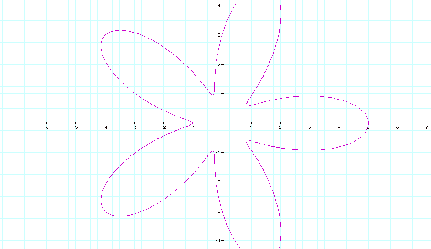
And finally when a and b are different with a < b, the rose begins to sprout another bloom!