Assignment 4
Investigation #5
Heather Robinson
EMAT 6680, Fall 2003
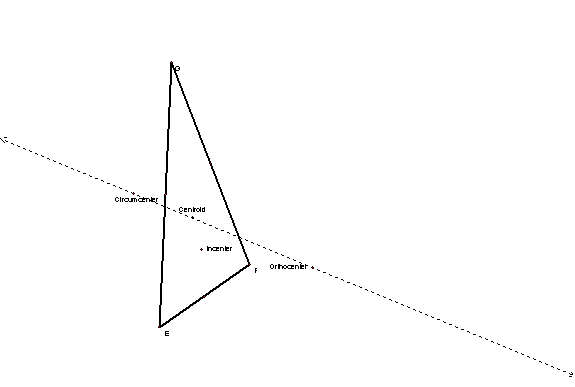
The triangle is an interesting geometric figure and exploring the many “centers” of a triangle is an extensive investigation. In this investigation, we have explored the centroid, circumcenter, orthocenter, and incenter of a triangle. Definitions for these centers are as follows…
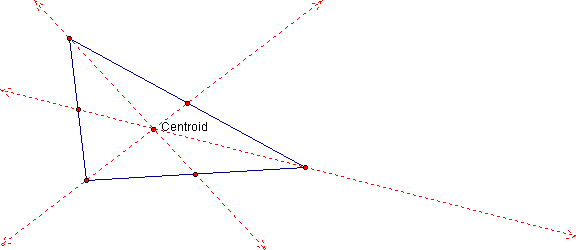
The centroid is defined as the point of concurrency for the medians in a triangle. The medians are the segments in a triangle created by connecting the midpoint of a side to the vertex of the angle opposite of the side. The medians are always on the triangle’s interior; therefore, the centroid will always be on the triangle’s interior.
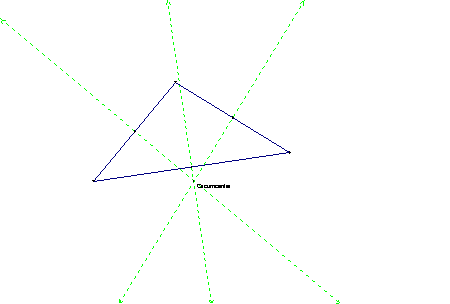
The circumcenter is the concurrency of the perpendicular bisectors. Perpendicular bisectors cut a side into two equal halves.
The orthocenter can be described as the concurrency of the altitudes. An altitude can be drawn from a vertex so that it is perpendicular to the opposite side. Altitudes may be inside or outside of the triangle; therefore, the orthocenter may be inside or outside of the triangle.

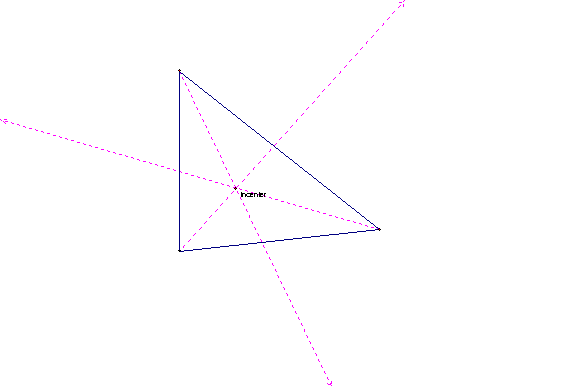
The incenter is the concurrency of the angle bisectors. Angle bisectors cut an angle into two equal halves.
The following facts hold true for the centroid, circumcenter, orthocenter, and incenter…
1. In an equilateral triangle, these four points are the same.
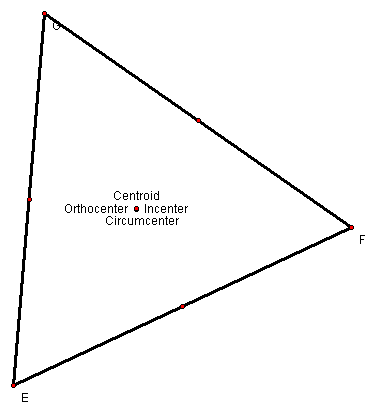
2. The circumcenter, centroid, and orthocenter are always collinear.
EXAMPLE 1
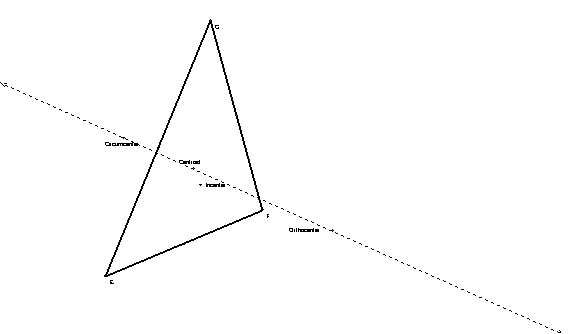
EXAMPLE 2