Assignment #6
Investigation #9
Constructing a Parabola Using a Trace of the Tangent Line
Heather J. Robinson
EMAT 6680, Fall 2003
Conic sections are represented in many of the shapes in the physical environment. Teaching conic sections without giving students a graphical perspective of how these shapes are created is quite unrealistic. Experiencing the construction of conic sections through hands-on experience and graphical analysis with Geometer’s Sketchpad is an excellent way to demonstrate the properties of these shapes.
This investigation will focus on the construction of a parabola using the line tangent to the curve. Prior to students experiencing this investigation with Geometer’s Sketchpad, students should construct a model of a parabola using paper folding (wax paper works best!). In the paper folding activity, students construct a line (the directrix) and an arbitrary point not on the line (the focus). Proceeding to create a series of folds by sliding the point not on the line along the line, a parabola is formed.
The following GSP investigation will be completed with students after the paper folding activity.
A parabola is the set of points equidistant from a line (called the directrix) and a fixed point (called the focus).
Construct a line in GSP and a point not on the line. These will serve as the focus and directrix respectively.
Beginning with this focus and directrix as such construct an arbitrary point on the Directrix.
The crease that was created in the wax paper construction by folding the focus onto the directrix at this arbitrary point on the line is shown below in green. This crease is the line tangent to the parabola.
In
order to simulate the series of creases created by continuing to move the focus
along the directrix, we must determine exactly where this crease will lie in
relation to the focus.
Constructing the midpoint of the segment between the arbitrary line and the focus shows that the crease seems to be the perpendicular bisector of this segment.
If the crease is the perpendicular bisector, it must pass through the midpoint of this segment form the Focus to the Arbitrary Point (AF).
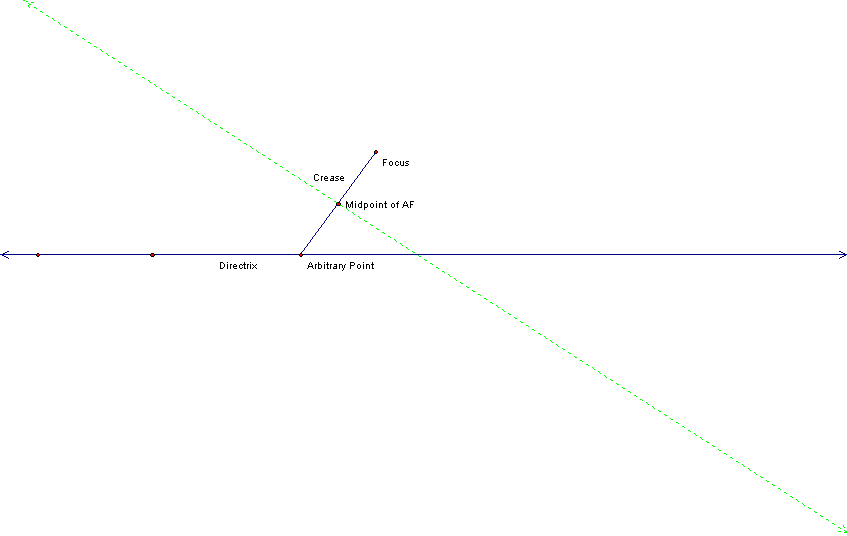The
crease does in fact pass through the midpoint, now let’s investigate whether
the crease is the perpendicular bisector.
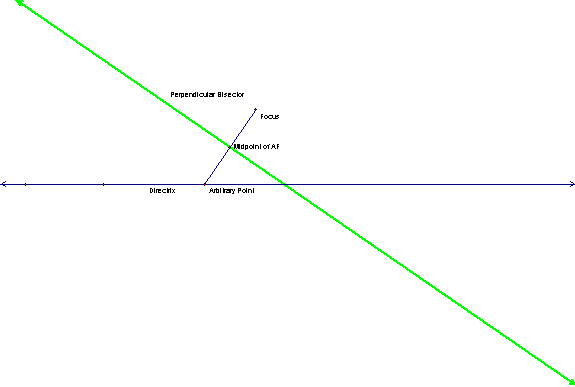Constructing
the perpendicular bisector of this segment confirms that the crease is exactly
this line!
Performing the trace of this tangent line as the arbitrary point slides back and forth along the directrix reveals the parabola!
