Assignment 8
Altitudes and Orthocenters

CONJECTURE
If H is the orthocenter of triangle ABC, then A is the orthocenter of triangle HBC and similarly B is the orthocenter of HAC and C is the orthocenter of triangle HAB.
REASONING
By definition, the orthocenter is the intersection point of the altitudes of each side in a triangle. Since H is the orthocenter, it follows that AH is perpendicular to BC, BH is perpendicular to AC, and CH is perpendicular to BA.
Let’s examine the
triangle HBC formed by orthocenter H and side BC of triangle ABC.
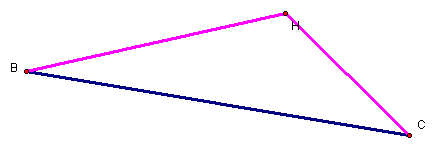
Constructing the altitudes for each side of this triangle shows that the altitude through H is AH, the altitude through C is AC, and the altitude through B is AB.

The orthocenter for triangle HBC is A.
It follows that B is the orthocenter of HAC and C is the orthocenter of triangle HAB.
ANOTHER OBSERVATION…
If any vertex of triangle ABC moves to where the orthocenter H is located, the circumcircle of ABC and the circumcircle of the triangle not including this particular point overlap. For example, moving point C such that C = H yields…
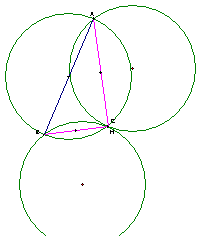
The circumcircle of HAB is overlapped by the circumcircle of ABC.
Also, the vertex that converges to H becomes the vertex of a right angle. In the previous picture, AB becomes the diameter of the circumcircle of ABC and the angle at C (or H) becomes a right angle. This is a phenomenon known as Thales’ Circle which states that if AB is a diameter of a circle with center M, then for any point C on the circle with center M, triangle ACB is a right angle.
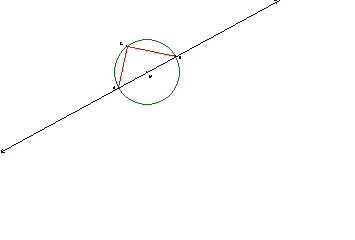
Proof:
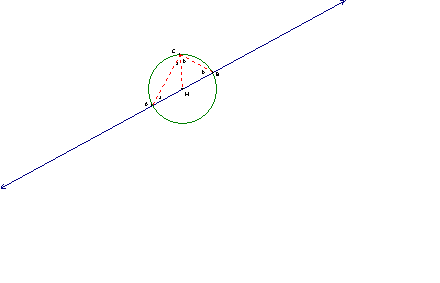
AM = MC (AMC is isosceles)
MB = MC (BMC is isosceles)
Define d = a
+ b
a + b + d = 180
a + b + (a + b) = 180
2a + 2b = 180
2 (a + b) = 180
a + b = 90
d = 90
PEDAGOGY
This assignment is rich in exploratory activities for geometry students. A major concept that is often left out of secondary geometry is the relationship between circles and triangles and how the properties of triangles can be derived on a circle. Students usually study geometry in pieces-basic geometry (point, line, plane), triangles (properties, similarity, congruence, and proof), and circles (properties). Rarely is there time to mesh these topics together and for students to experience and discover the properties that triangles and circles have in common. The exploration moving the vertices of triangle ABC onto H is particularly interesting because several important topics like chords, right triangles, and altitudes are all incorporated.