FINAL ASSIGNMENT
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
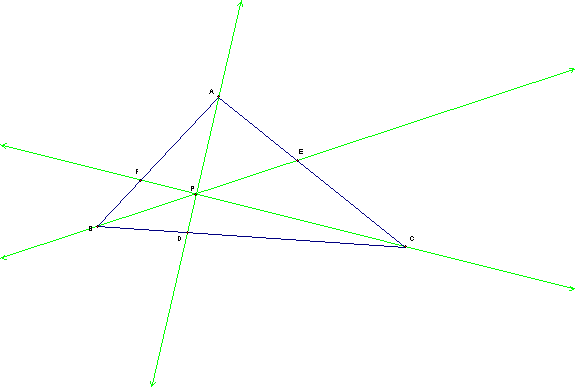
Explore
(AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
We can begin by picking an arbitrary point P and finding the value of
(AF)(BD)(CE) and (BF)(CD)(AE).
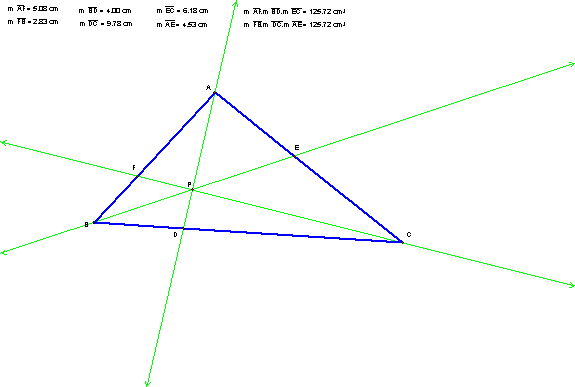
At this particular location, (AF)(BD)(CE) = (BF)(CD)(AE) and the ratio
(AF)(BD)(CE) /(BF)(CD)(AE) = 1.
Click here to manipulate the sketch to move A, B, C, and P around!
Conjecture: As long as P remains inside the triangle, this ratio of the products
(AF)(BD)(CE) /(BF)(CD)(AE) = 1.
To prove this conjecture, let’s examine when P is the centroid of the triangle…
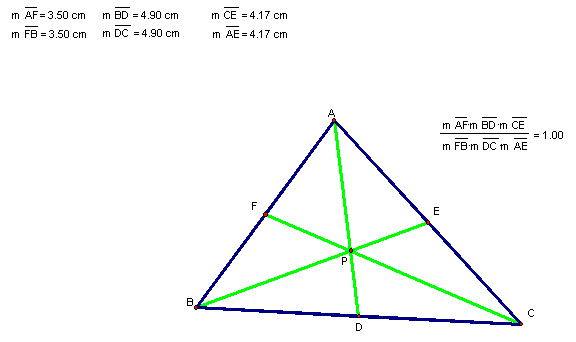
We can construct a line parallel to BC through A in order to create some similar triangles.
If we choose these pairs carefully, we can prove our result!
Similar Triangles
BDP is similar to HAP,
CEB is similar to AEH,
BFC is similar to AFG, and
GAP is similar to CDP
Yields the following relationships…
BD/HA = PD/PA,
CE/AE = CB/AH,
AF/BF = AG/BC, and
GA/CD = PA/PD.
We
can create an equation ![]() .
.
Simplifying…
![]()
Multiply
both sides by ![]() to get…
to get…
![]()
When P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?
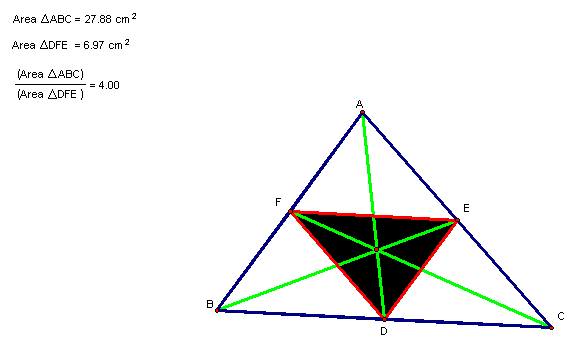
The ratio of the areas is equal when P is the centroid!!!