Examining Linear Equations and Their Products

By

Janet M. Shiver

EMAT 6680

Investigation:  Find two linear function f(x) and g(x) such that their product is tangent to each of f(x) and g(x) at two distinct points.

Before beginning the investigation it is important to define linear function and quadratic function.

A linear function will be defined as a function of the form y = mx + b, where m represents the slope of the line defined by the function and b represents the y-intercept.

A quadratic function will be defined as a function of the form , where a, b and c are constants.

Step One:  I began examining linear equations of the form y = b (where m = 0) and their product.

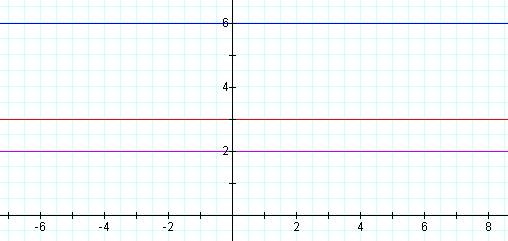
Here we see a graph of  f(x) = 2, g(x) = 3 and their product f(x)*g(x) = 6.

This first investigation did not yield the desired results.  Since all three of the lines are horizontal and thus parallel to one another, there is no possibility of the functions f(x) and g(x) intersecting the function of their product f(x)*g(x). 

Step Two: Next, I examined linear equations of the form y = mx and their product.  You will notice that since the y-intercept equals zero, both f(x) and g(x) pass through the origin.

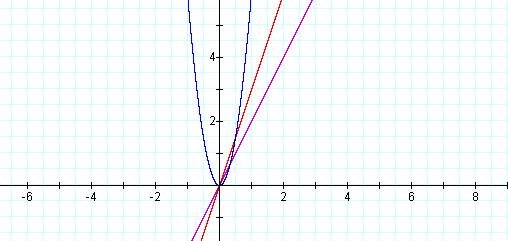
Here we see a graph of f(x) = 2x, g(x) = 3x and f(x)*g(x) =

In this second attempt we see that the product of the linear functions f(x) and g(x) did produce a parabola.  The reason for this is that the linear functions that were chosen were of the form y = mx.  When two linear equations of this form are multiplied the result is a quadratic equation of the form y = for some constant a.

Although this attempt is closer to the desired result, there are still several difficulties that have to be addressed. We will begin with the linear functions f(x) and g(x).  Both of these functions currently have positive slopes; however, the desired graph shows one line with an increasing slope and the other with a decreasing slope.

Step Three:  For my third attempt I chose one linear function with a positive slope and one with a negative slope.

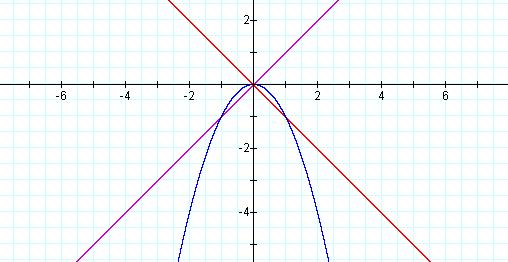
Here we see a graph of f(x) = x, g(x) = -x and f(x)*g(x) =

It appears that we are closing in on the desired result.  We now have an increasing linear function and a decreasing linear function whose product results in a quadratic equation. The graph of the quadratic equation is a parabola that is concave downward.  Since the parabola intersects the x-axis at a single point, we see that it has only one root. Now we need to address the issue of tangency.  Clearly, the current graph shows that both f(x) and g(x) intersect their product at two points, neither of which are points of tangency.

Step Four: To address the points of tangency we will examine several graphs of linear functions that have been shifted vertically.  We will begin by shifting both f(x) and g(x) upward.

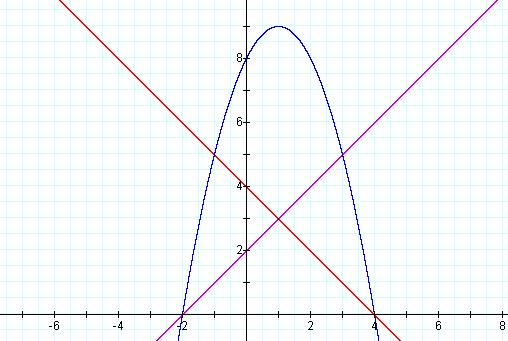
Here we see a graph of f(x) = x+2, g(x) = -x + 4, and f(x)*g(x) =

Although we did not achieve our goal of tangent functions, we can see another interesting fact.  From this graph we notice that the lines intersect the parabola at its x-intercepts or roots.  This occurs because the quadratic equation is obtained from the product of the two linear functions.  In this case f(x)*g(x) = (x +2)(-x + 4).

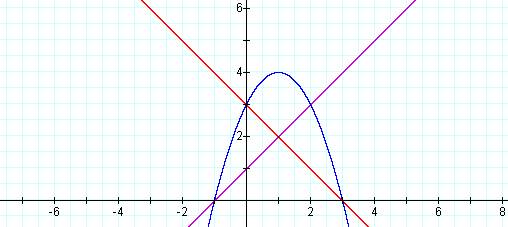
Here we see a graph of f(x) = x+1, g(x) = -x+3, and f(x)*g(x) =

Although this graph is a little better, we have still not found lines that are tangent to the graph of their product. Notice, however, that once again the graphs of the lines intersect the graph of the parabola at the parabola’s x- intercepts or roots.

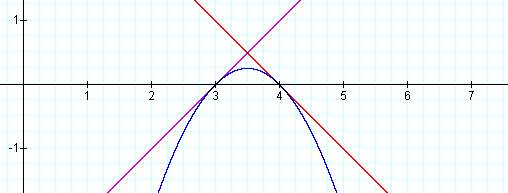
Here we see the graph of  f(x) = (x-3) and g(x) = (-x+4) and f(x)*g(x) =

Victory!  We have now found two linear functions whose graph of their product is tangent to each of the two linear functions at two distinct points.

It appears that by reducing the distance between the x-intercepts of the parabola the graphs have now become tangent at these points.

Let’s try one more. We will once again keep the distance between the x-intercepts at one unit.

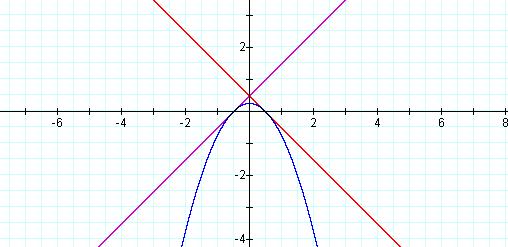
Here we see the graph of 

Once again we appear to be successful!  So for linear equations of the form y = mx +b, where m is either one or negative one it appears that for the two linear equations to intersect the parabola such that they are tangent to the parabola formed by their product, the lines must have a slope of one but have different directions.  It also appears that the distance between the x-intercepts must be one.

Finally, we will investigate what happens to the parabola as the slopes of the linear equations vary.

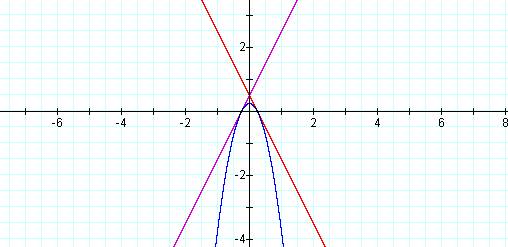
Here we see the graph of 

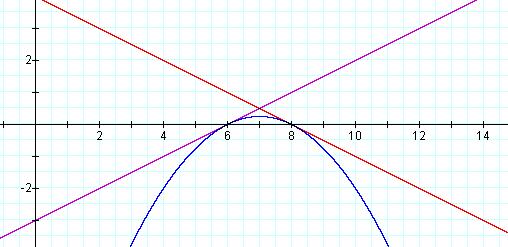
                        Here we see the graph of f(x) = 1/2x-3, g(x) = -1/2x+4, and f(x)*g(x) = -

We notice that the distance between the x-intercepts appears to have a reciprocal relationship with the slope of the lines.  In the first graph we see that the lines have a slope of  ±2  and the distance between the x-intercepts (roots) is ½. In the second graph we have a slope of ±1/2 and a distance of 2.

Return to Janet Shiver’s Home Page