Field Goal

By

Janet M. Shiver

EMAT 6680

Investigation

The rules in college football were changed a few years ago, making the uprights five feet narrower than in previous years.  Many game commentators have harped about how much harder it is to kick field goals from the hash marks.  Assume the field goal is attempted from the hash marks.

At what yard marker does the kicker have maximum angle to the two uprights? 

Is there any merit to some commentator’s argument to take a penalty in order to have a “better angle” on the field goal kick?

To determine which yard line is best for kicking a field goal from the hash click here.  Move the football up and down the hash marks while watching the angle measure.

Scroll down for the solution.

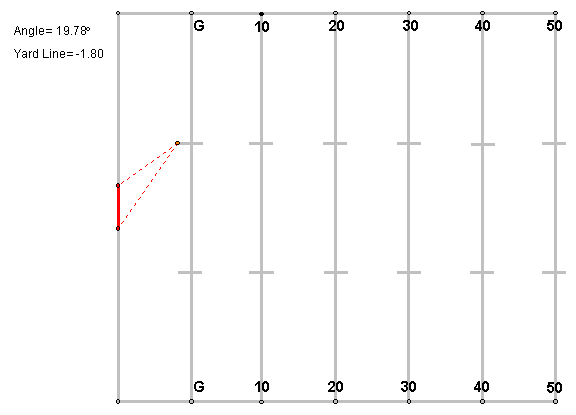
It appears that the ball should be place approximately 2 yards off the goal line into the end zone.

Next, lets take a look at the problem from a trigonometric standpoint and try to develop a function to represent this angle. 

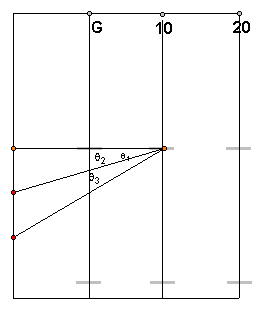
First notice that two right triangles have been formed on the field. Using the tangent function and the diagram above, we can see that

Solving each equation for , we get . 

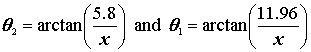Since , 

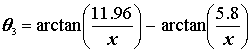
A graph of this function appears below.

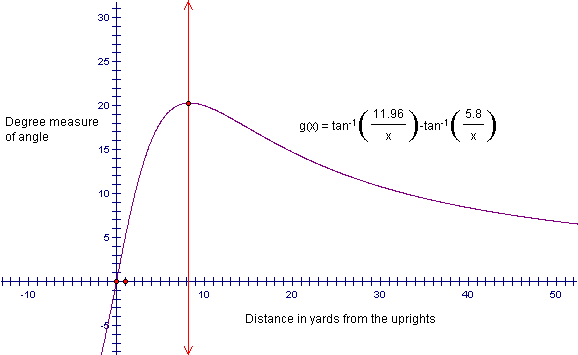
We can see from the graph that the point at which the angle reaches its maximum occurs when x equals approximately 8.  That is the angle reaches its maximum when the football is two yards past the goal line in the end zone.

Finally, lets take a look at this problem geometrically.

We are going to construct a circle through points A, B and C.  To do this we must first determine the midpoints of the sides of triangle ABC and then construct perpendicular lines through this point.

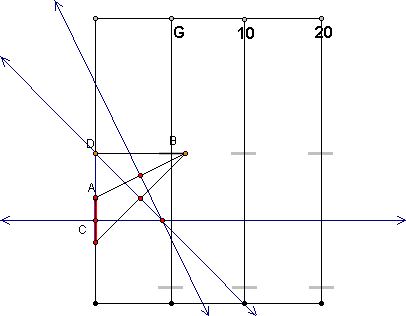
The intersection of the three perpendicular lines determines the center point for our circle.

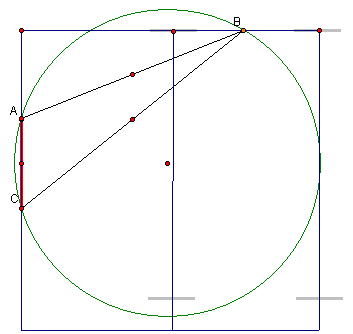
The angle we want to maximize is angle ABC and since it is an inscribed angle we know that it is ½ the measure of its intercepted arc AC.  It follows that if we maximize arc AC then we will also maximize angle ABC.

Click Here and move point B to determine when the arc is maximized.

It appears that the arc is maximized when the area of the circle is minimized.  This occurs when the circle is tangent to the hash marks.

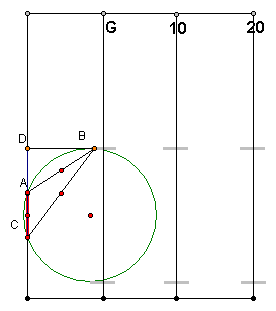
This point of tangency appears to take place approximately 8 yards from the uprights. 

From our investigation, it appears that the best place to kick a field goal from the hash marks is two yards into the end zone.  Since this is not a possibility in the game of football, we can conclude that the closer a kicker is to the goal line the better the angle will be for his kick.

Return to Janet Shiver’s Home Page