Tangent Circles
†
By
Janet M. Shiver
EMAT 6680
†
†
†
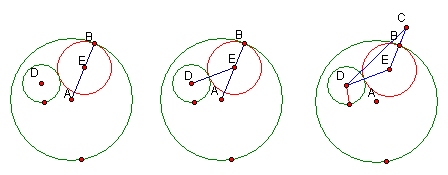
Investigation:† Given two circles and a point on one of the circles.† Construct a circle tangent to the two circles with one point of tangency being the designated point.
†
†
![]() †
†
†
†Tangent Circles.
†
Before we begin
our construction of tangent circles we must first understand the approach
we will be taking.† The basic idea behind our construction
is that given any two circles, say A and D, and a third circle E that is
tangent to both A and D, then the center point of E must lie along the radius
of one of the circles (see figure 1).† Also note that
the length of the segment connecting the centers D and E is the sum of the
radii of circle D and circle E (see figure 2).† Imagining
that this is the length of the leg of an isosceles triangle, we will construct
another leg of equal length through points E and B.† To
do this we must add the length of the radius of circle D to the radius of
circle E along segment EB (see figure 3).
†
†
†
We can now see
that if we found the midpoint of CD that the line through the midpoint and
the center point E of the tangent circle would be the perpendicular bisector
of the base of the isosceles triangle.† We can clearly
see that the center point of the tangent circle can be found at the intersection
of this perpendicular line and the line through EC.
†

†
†
Construction of Tangent Circles
†
Draw two circles and
place a point, A, on the large circle.
†
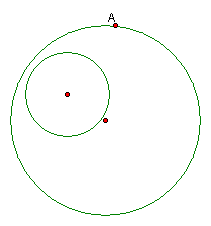
†
Construct a line through the center point B of the larger circle, and point A. †Also construct a segment representing the radius of the smaller circle.
†
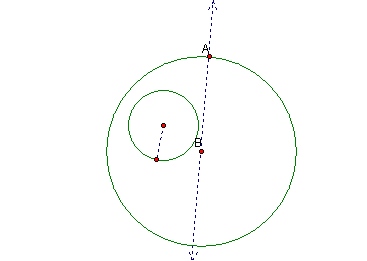
†
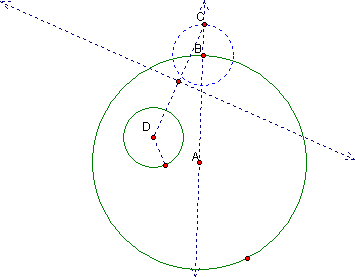
Construct a circle with center point a and a radius of the same length as the small circle.† Label the point of intersect (outside the large circle) of the new circle and line AB as C.
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
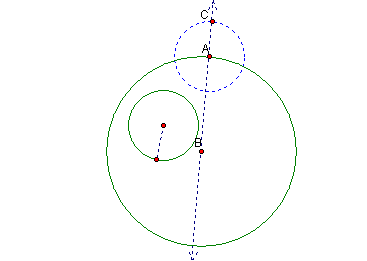
†
Now connect the center of the small circle with point C forming segment DC.† Find the midpoint of segment DC and construct a perpendicular through this point.
†
†
Finally, mark the point of intersection between the two lines.† This will become the center point of the tangent circle.† Now construct the final circle using the center point E and the radius EB.
†
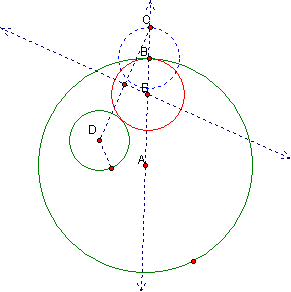
†
†Click Here to see an animation of the construction.
Using a similar construction we can find a second circle that is tangent
to both of the original circles.
†
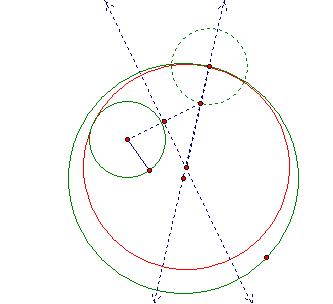
†
†
†
†
Locus of Points
†
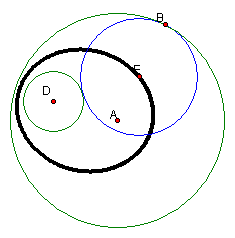
Now lets examine the loci of the center of the
tangent circles for each of our cases.
†
 † ††††††††††††††††††††††††
† ††††††††††††††††††††††††
†
Clearly, the locus of points formed by the center
of the tangent circle is an ellipse. It appears that the centers of the two
original circles are the foci of the ellipse.† Looking
at our second construction, we see that if D and A are the foci then the
sum of the distances between DE and AE must stay consistent.† Click Here and
animate the construction to see the measurement of segment DE, segment AE
and their sum.
†
†
†
†
†
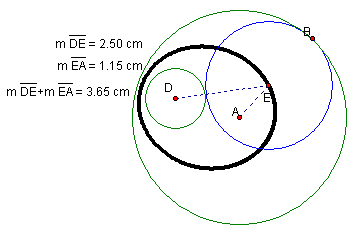
After animating the diagram, it was clear that
as the length of segments DE and AE varied their sum was always 3.65cm.
†

After animating the diagram of our second construction,
it was clear that as the length of segments GI and HI varied their sum was
always 2.03cm.
†
†
Overlapping Circles
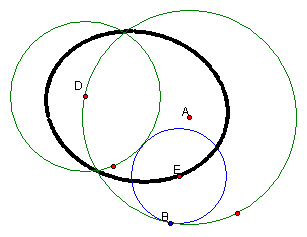
†
We also achieve the same results when the two original
circles are overlapping.† Notice once again that the
center points of ours original circles appear to be the foci for the ellipse
formed by the locus of points created by the center of the tangent circle.
†
†
†
†
Disjoint Circles
†
Now letís examine the case where the original circles
are disjoint.† As we can see from the construction
below the results are quite different from our other constructions.† Instead of a parabola, the locus of points generated by
the center point of the tangent circle produces a hyperbola. It appears that
the center point of the two original circles are the foci of the hyperbola.

To support our conjecture, we will measure the length of segment DE and segment AE and then find the absolute value of their difference.† Click Here and animate the construction to see the measurement of segment DE, segment AE and their difference.
†
†
†
†
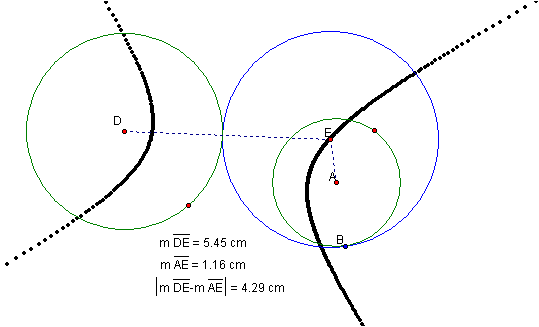
†
After animating the diagram of our construction, it was clear that as the length of segments DE and AE varied the absolute value of their difference was always 4.29cm.
†