Ratios, Altitudes and Orthocenters
By Janet M. Shiver and Blair Dietrich
EMAT 6680
Investigation: During this investigation we will be looking at the altitudes and orthocenters of various triangles. We will then prove for any acute triangle and its circumcircle, that by extending its altitudes until they intersect the circumcirle at corresponding points P, Q and R that the measure of
![]() .
.
To begin our investigation
we will construct several triangles and their orthocenters. Lets start with
any acute triangle ABC and construct its orthocenter H. Remember, the orthocenter
of a triangle is the common intersection of the three lines containing the
altitudes of the triangle.
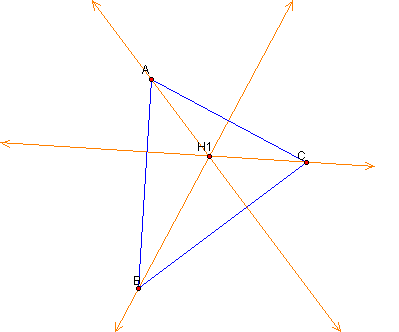
Now we will construct
the orthocenter for the newly formed triangle ABH1.
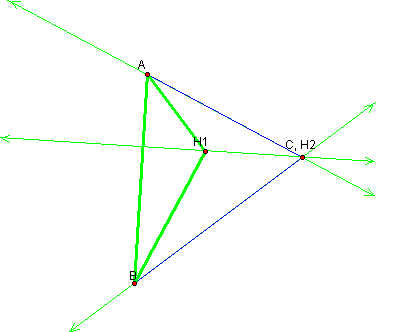
Notice that the orthocenter
for triangle ABH1 is the vertex C of the original triangle ABC.
Next we will construct
the orthocenter for triangle ACH1.
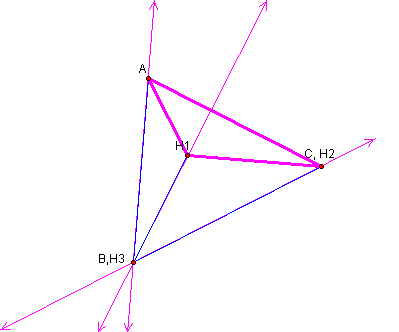
Notice that the orthocenter for triangle ACH1 is the vertex B of the original triangle ABC.
Finally, we will construct
the orthocenter for the newly formed triangle BCH1.
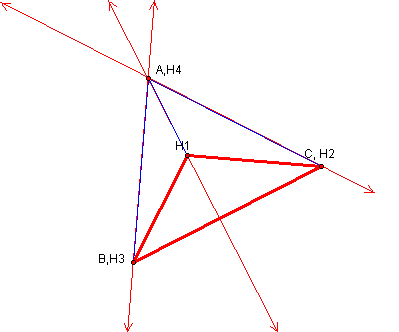
Once again, you will notice that the lines containing the altitudes of our newly formed triangle intersect at one of the vertices of the original triangle ABC, this time at vertex A.
Lets take a look at
the circumcircles for all four of our triangles.
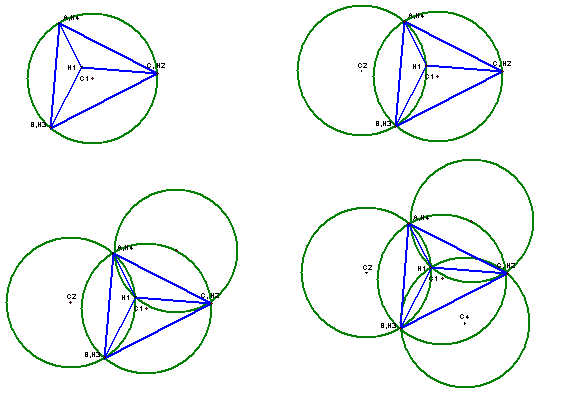
We can see that all
of the circumcircles appear to be the same size for each of the constructed
triangles.
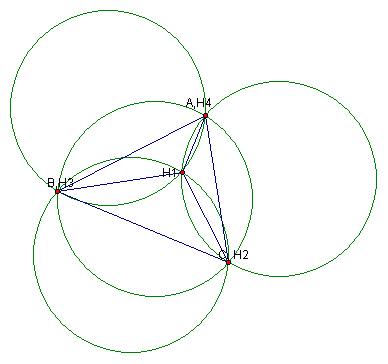
As we change the shape of our triangle, we can see that the circumcircles continue to be the same size. Click Here to see for yourself.
Now lets see what
happens if we move one of the vertices to the orthocenter of triangle ABC.
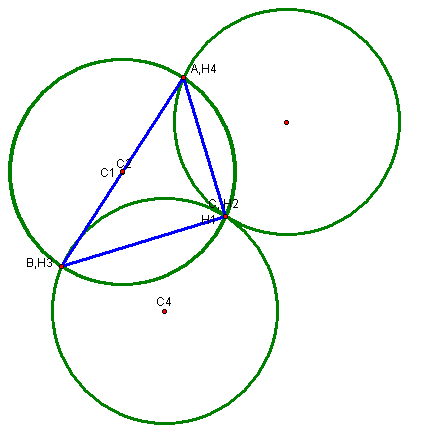
We can see that one of the circles completely overlaps the circumcircle of the original triangle ABC. Why? This occurs because the orthocenters of the smaller triangle lies on the vertex of the original triangle. So when the orthocenter of the smaller triangle is moved to the orthocenter of the original triangle a single right triangle is formed.
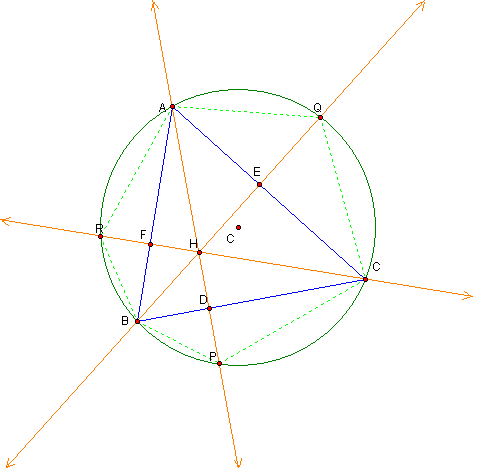
Next we would like to investigate the relationship between the altitudes of an acute triangle and their extensions as they intersect the circumcircle.
We will begin by constructing an acute triangle ABC and its circumcircle.
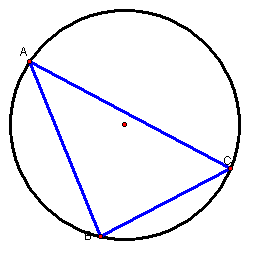
Next we will construct the altitudes of the triangle and extend them using lines.

We will now prove for any acute triangle ABC and its circumcircle, that by extending its altitudes until they intersect the circumcirle at corresponding points P, Q and R that the measure of
![]() .
.
By construction we
will draw segments BP, CP, AR, BR, AQ, and CQ.
We will show that triangle BCP is congruent to triangle BCH, triangle ARB is congruent to triangle AHB and triangle AQC is congruent to triangle AHC.
We will begin with triangles BHC and BPC. First we will dilate the circumcircle by ˝ about the orthocenter. This becomes the nine point circle of triangle ABC. Since it is ˝ the diameter of the original triangle ABC and it passes through point D, then HD = 1/2HP.
By segment addition HP = HD+DP,
Using substitution HD =1/2(HD + DP)
HD = 1/2HD +1/2DP
1/2HD = 1/2DP
HD = DP
Since AD is an altitude
of triangle ABC then it intersects BC at a right angle, thus angle HDB and
angle HDC are right angles and have an angle measure of 90 degrees.
By supplementary angles,
angle HDB + angle PDB = 180 degrees
Using substitution,
90 degrees + angle PDB = 180 degrees
angle PDB = 180 degrees – 90 degrees
angle PDB = 90 degrees
Similarly, it can
be shown that angle HDC + angle PDC = 180 degrees and hence angle PDC = 90
degrees.
Thus, angle HDB =
angle PDB and angle HDC = angle PDC.
By the reflexive property
BD = BD and DC = DC.
By the side, angle,
side congruence property, triangle HDB is congruent to triangle PDB and triangle
HDC is congruent to triangle PDC.
Since congruent parts
of congruent triangles are congruent, angle HBD is congruent to angle PBC
and angle HCD is congruent to angle PCD.
By the reflex property
BC is congruent to BC.
Thus, by the angle-side-
angle congruence property, triangle BPC is congruent to triangle BHC.
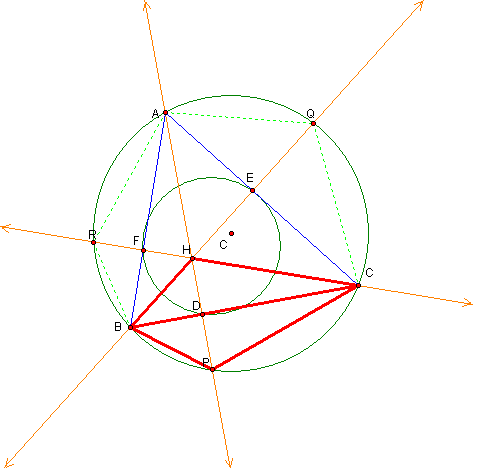
Using a similar argument we can show that triangle APB is congruent to triangle AHB and triangle AQC is congruent to AHC.
Therefore, since triangle BHC is congruent to triangle BPC, triangle APB is congruent to triangle AHB and triangle AQC is congruent to AHC, twice the area of triangle BPC + twice the area of triangle BRA +twice the area of triangle AQC equals twice the area of triangle ABC
Notice, that by multiplying
any of the altitudes and the side to which they are perpendicular we will
always get twice the area of the triangle. For ease of notation, we will
be assigning x equal to twice the area of triangle ABC.
![]() =
=
![]()
= ![]()
= 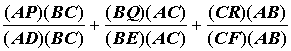
Note: (AD)(BC) = (BE)(AC)
= (CF)(AB) = twice the area of triangle ABC = x.
= ![]()
By segment addition,
AP = AD + DP, BQ = BE + EQ and CR = CF + FR.
Substituting we obtain,
![]()
= ![]()
=![]()
= ![]()
= ![]()
= ![]()
= 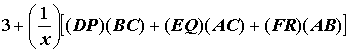
Since ![]() the
area of triangle ABC
the
area of triangle ABC
Then, 2![]() = twice the area of ABC = x
= twice the area of ABC = x
Thus, using substitution
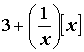
= 3 + 1 = 4.
Therefore, we have proved for any acute triangle ABC and its circumcircle, that by extending its altitudes until they intersect the circumcirle at corresponding points P, Q and R that the measure of
![]() .
.
Return to Janet Shiver's Home Page