EMAT 6680

Investigation: We will be examining the various properties of pedal triangles.

Construction of a Pedal Triangle

Construct any triangle. Place a point P in the plane.

2. Construct perpendicular lines from point P to the sides of the triangle and mark the points of intersection.

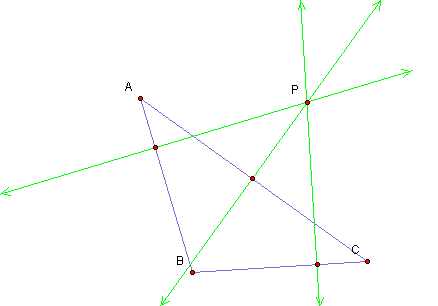
3. Connect the points of intersection to form a new triangle. This triangle is called the Pedal Triangle and point P is referred to as the Pedal Point.

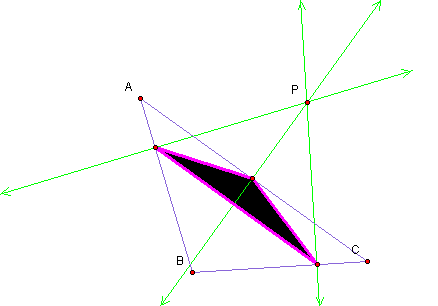
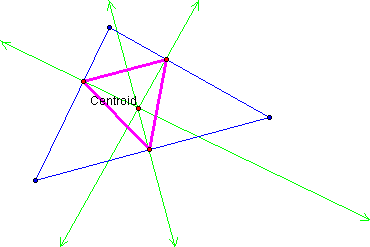
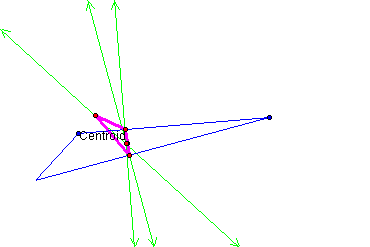
What if the pedal point is the centroid of the triangle?

It appears that, for many triangles ABC, the pedal triangle will lie inside the original triangle. However, this is not the case for all triangles. As you can see below, for some obtuse triangles the pedal triangle does not fall completely within the original triangle.

What if the pedal point is the incenter? Click here to investigate. Move the pedal point to the incenter. What happens to the pedal triangle?

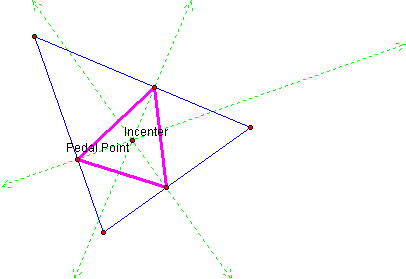
It appears that as the pedal point becomes the incenter of a triangle, the incenter will lie equidistant from each of the vertices of the pedal triangle. We can see this more clearly when we construct the incircle of the triangle.

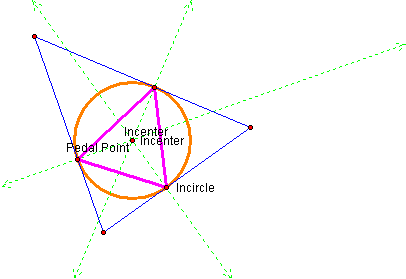
Notice that the vertices of the pedal triangle all lie on the incircle. This indicates that the segment from the incenter of the blue triangle to any vertex of the pedal triangle becomes the radius of the incircle.

What if the pedal point is the orthocenter? Click here to investigate. Move the pedal point to the orthocenter. What happens to the pedal triangle?

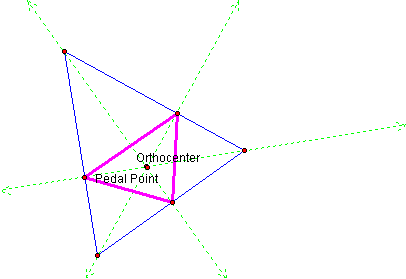
First we will examine what happens when the orthocenter is inside the triangle. Here it appears that, as the pedal point becomes the orthocenter of the triangle, the vertices of the pedal triangle have become the feet of the altitudes of the blue triangle. This would imply that the pedal triangle has become the orthic triangle.

But what if the orthocenter is outside the triangle?

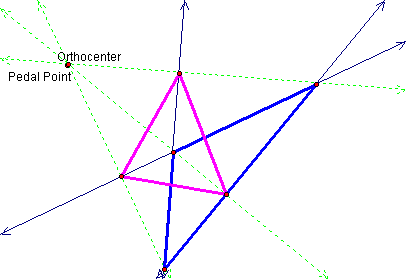
By extending the sides of our triangle we can see that the same results hold. The pedal triangle is the orthic triangle.

What if the pedal point is the circumcenter? Click here to investigate. Move the pedal point to the circumcenter. What happens to the pedal triangle? Change the shape of your triangle and try again.

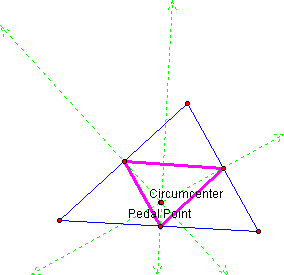
Notice that, as the pedal point was positioned over the circumcenter, the perpendicular lines of the pedal triangle appear to be passing through the midpoints of the blue triangle. This would imply that the pedal triangle has become the medial triangle. We can also see that the blue triangle is now divided into four congruent triangles. This would mean that the area of the pedal triangle is now ¼ the area of the blue triangle.

What happens if the circumcenter is outside the triangle?

It appears that the same results hold. The pedal triangle has once again become the medial triangle and has divided the blue triangle into four congruent triangles.

What happens when the pedal point is moved to a vertex of the blue triangle? Click Here to investigate. Move the pedal point to a vertex. Now move it to the other vertices. What did you find?

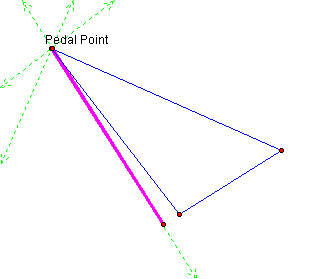
When the pedal point becomes one of the vertices the pedal triangle collapses into a line segment. Here we see that the three vertices of the pedal triangle are now collinear. The line they have formed is called the Simson line. The Simson line is formed when all three vertices of the pedal triangle are collinear and the pedal triangle is a degenerate triangle. We can see that this happens at the vertices of the triangle but does it occur anywhere else?

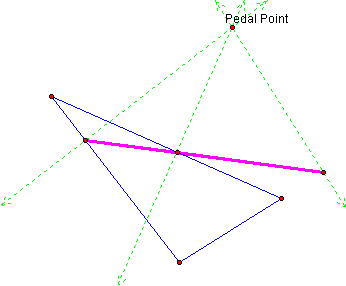
The Simson line is also present when one of the vertices of the pedal triangle passes through the side of the blue triangle.

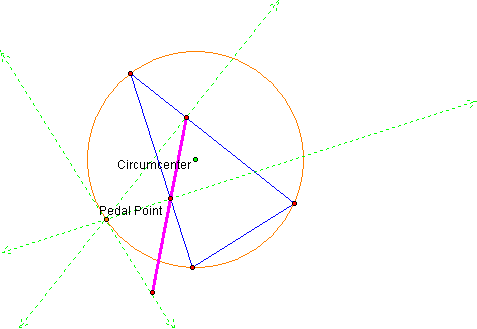
By constructing the circumcircle we see that any time the pedal point lines on the circle, the pedal triangle will degenerate and become the Simson line. Click Here to try it.

Next lets trace our Simson line as the pedal point moves around the circumcircle of our triangle. As we can see the envelope of the Simson line is a deltoid.

Finally, lets complete our investigation by tracing the midpoints of the sides of the pedal triangle as our pedal point travels in a circular path. First lets see what happens as our pedal point travels around the circumcircle.

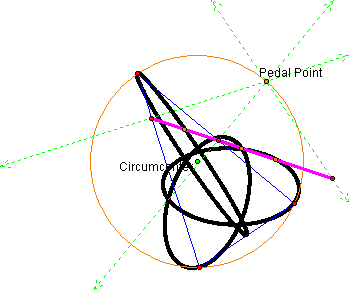
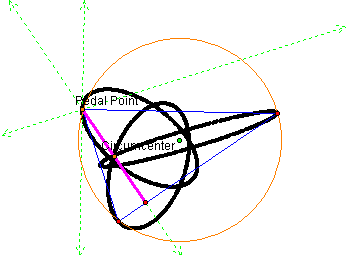
It appears that the locus of the midpoints form three ellipses. Also, we can see below that the Simson line forms the altitude of the triangle when the pedal point passes through each of the vertices.

Another observation that can be made is, at three different times the Simson line becomes one of the sides of the triangle. To see when this occurs we will construct the midpoints of the blue triangle.

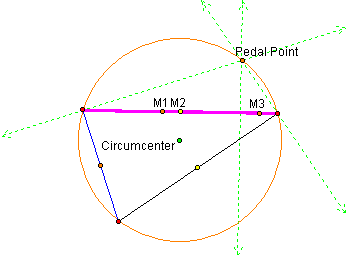
The Simson line (segment) becomes a side of the triangle when the midpoints of the pedal triangle and the midpoints of the original triangle coincide. Click Here to see for yourself.

One final observation.

If we examine a right triangle in which the pedal point is animated around its incircle we find that one of our three elliptical paths becomes a circle.

Return to Janet Shiver’s Home Page