

2. Make up linear functions f(x) and g(x).
Explore, with different pairs of f(x) and g(x) the graphs for
i. h(x) = f(x) + g(x);
ii. h(x) = f(x).g(x);
iii. h(x) = f(x)/g(x);
iv. h(x) = f(g(x));
Summarize and illustrate.
i. h(x) = f(x) + g(x)
Consider the following examples:
a. f(x) = 2x + 1 , g(x) = x - 3 , h(x) = 3x - 2
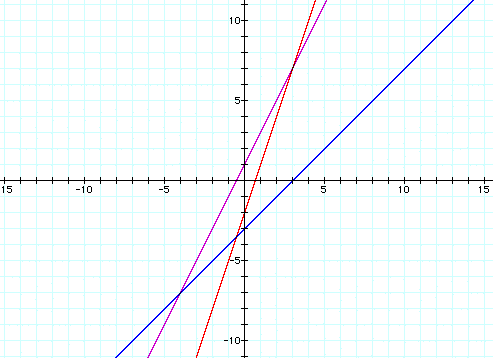
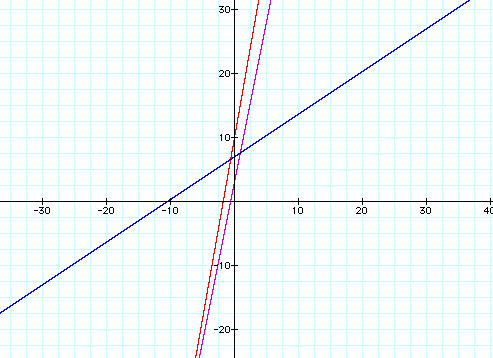
b. f(x) = 5x + 3 , g(x) = 2/3 x + 7 , h(x) = 17/3 x + 10
c. f(x) = -3x - 6 , g(x) = x + 4 , h(x) = -2x - 2
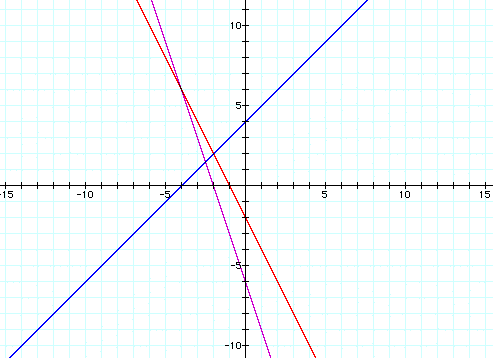
There are a couple of things to note from these examples. The y-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept. When you add two linear functions, you are combining like terms. In other words you add the slopes and then add the y-intercepts. Let's first look at the y-intercepts. These graphs clearly illustrate that the sum of the two original y-intercepts is equal to the y-intercept of h(x). In example a, 1 + (-3) = -2 and h(x) = 3x - 2. Now let's consider the slopes. The relationship of the slopes is not as easy to see on the graphs. If you consider the slope as the steepness of the line, then examples a and b show that h(x) is the steepest. You can observe that by combining the slopes of the two original equations, the sum of the slopes is greater and thus the line is the steepest. These two examples were special cases since both of the original slopes were positive. However, in example c one of the slopes is negative. This relationship is more difficult to see.
ii. h(x) = f(x).g(x)
Consider the following examples:
a. f(x) = 2x + 1 , g(x) = x - 3 , h(x) = 2x^2 - 5x - 3
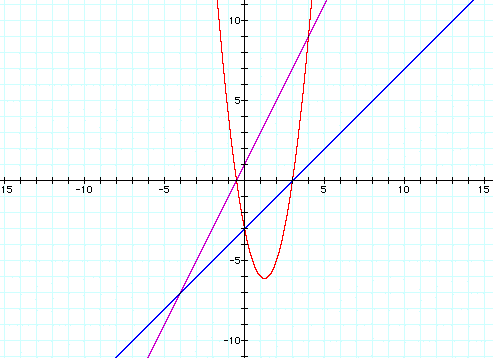
b. f(x) = 5x + 3 , g(x) = 2/3 x + 7 , h(x) = 10/3 x^2 + 37x + 21
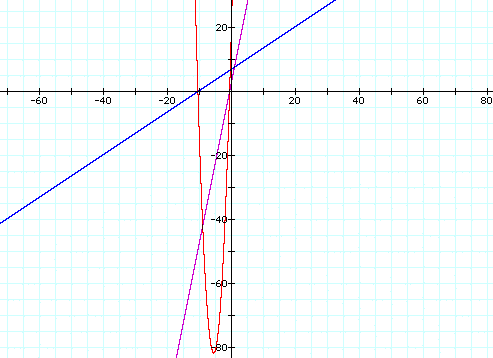
c. f(x) = -3x - 6 , g(x) = x + 4 , h(x) = -3x^2 - 18x - 24
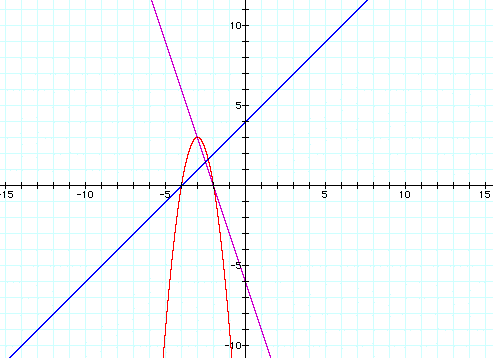
In this section we have multiplied two linear functions together to get a quadratic function, so the graphs have two lines and a parabola. We can see an interesting relationship immediately. The x-intercepts of the parabola are the same as the lines. We know that x-intercepts on a graph represent the roots of the equation. Therefore, the roots of the parabola are equal to the x-intercepts of the lines. We usually find the roots of a quadratic equation by factoring, which is the inverse operation of multiplication. So, when we multiply two linear functions, we are expanding the roots of the quadratic. We also like to consider the vertex of the parabola. We know that a parabola is symmetric about its vertex, so we can find the x-coordinate of the vertex by finding the midpoint of our two x-intercepts. This relationship is easy to see on the graphs.
iii. h(x) = f(x)/g(x)
Consider the following examples:
a. f(x) = 2x + 1 , g(x) = x - 3 , h(x) = (2x+1) / (x-3)
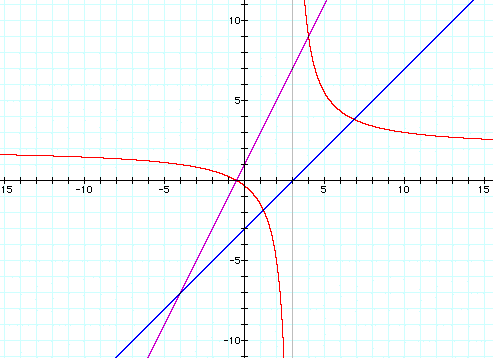
b. f(x) = 5x + 3 , g(x) = 2/3 x + 7 , h(x) = (5x + 3) / (2/3 x + 7)
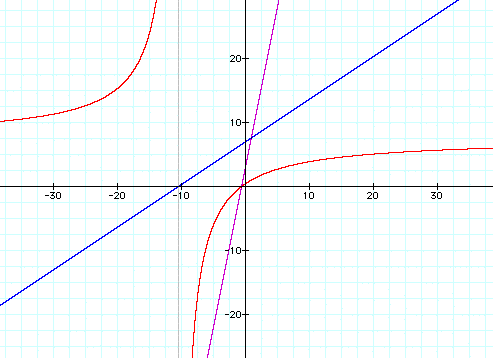
c. f(x) = -3x - 6 , g(x) = x + 4 , h(x) = (-3x - 6) / (x + 4)
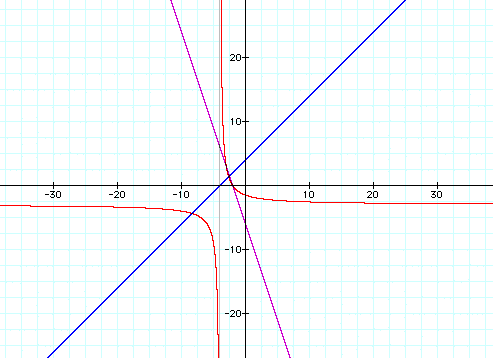
In these examples we have divided two linear equations and the result on the graph is a hyperbola.
iv. h(x) = f(g(x))
Consider the following examples:
a. f(x) = 2x + 1 , g(x) = x - 3 , h(x) = 2x-5
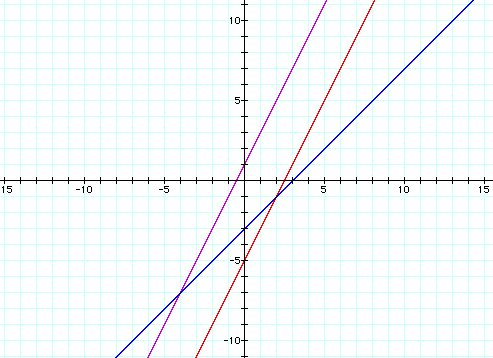
b. f(x) = 5x + 3 , g(x) = 2/3 x + 7 , h(x) = 10/3 x + 38
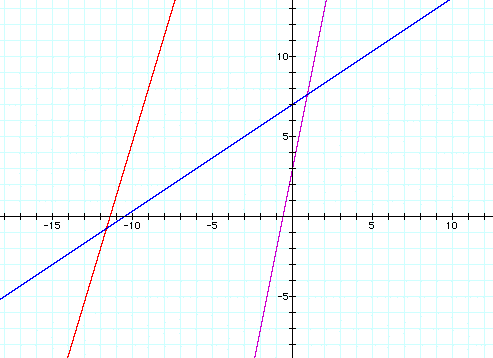
c. f(x) = -3x - 6 , g(x) = x + 4 , h(x) = -3x - 18
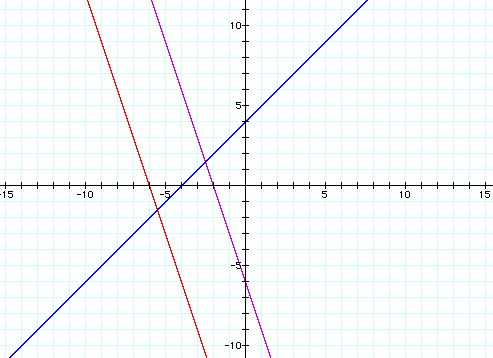
In these examples we have found the composition of two linear functions. The graph of the composition is a line. An interesting discovery from examples a and c is that if g(x) has slope of 1, then the composition is parallel to f(x). Anytime we find the composition of two linear functions, the slope of the composition is the product of the original slopes. This is difficult to see on the graph. However, we can make the following conclusions: if both slopes are positive, the composition slope will be positive; if both slopes are negative, the composition slope will be positive; and if one only of slopes is positive, the composition slope will be negative.