Exploring the Circumcenter

by

Mindy Swain

Assignment 4:

#3. The circumcenter (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Note: C may be outside of the triangle.

Construct the circumcenter C and explore its location for various shapes of triangles. It is the center of the circumcircle (the circumscribed circle) of the triangle.

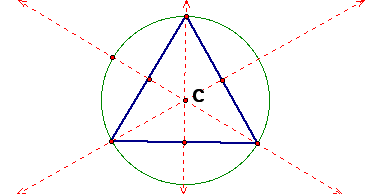
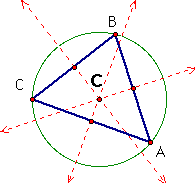
i. My first example is an equilateral triangle, a special case of an acute triangle. The perpendicular bisectors for each side intersect with the opposite vertex. The circumcenter, C, lies on the inside of the triangle. I have also constructed the circumcircle of the triangle.

Click on the image above to open this GSP document and explore these properties for yourself.

Here are some other cases of acute triangles where similar observations can be seen:

(The perpendicular bisectors do not intersect with the opposite vertex, but the circumcenter is still inside the triangle.)

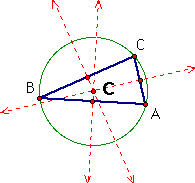
ii. Now I have an obtuse triangle. The circumcenter, C, is outside of the triangle since the perpendicular bisectors intersect outside of the triangle. I have also constructed the circumcircle of the triangle.

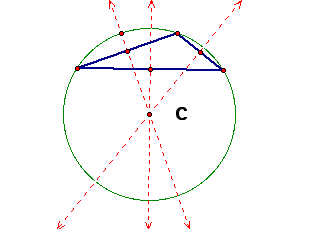
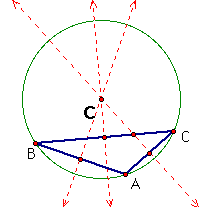
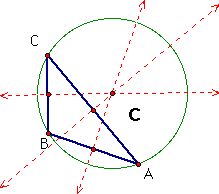
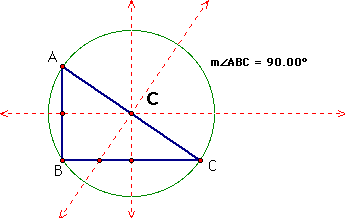
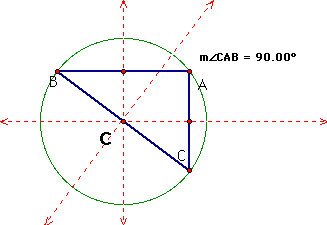
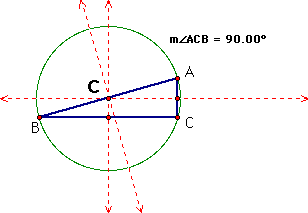
Here are some other cases of obtuse triangles where similar observations can be seen:

iii. Here is a right triangle. The circumcenter, C, intersects the midpoint of the hypotenuse. In this case the hypotenuse of the triangle is a diameter of the circumcircle.

Here are some other cases of right triangles where similar observations can be seen:

Return