

#2. If the original triangle is equilateral, then the triangle of medians is equilateral. (1) Will an isosceles original triangle generate and isosceles triangle of medians? (2) Will a right triangle always generate a right triangle of medians? (3) What if the medians triangle is a right triangle? Under what conditions will the original triangle and the medians triangle both be right triangles?
(1) Triangle ABC is an isosceles triangle and triangle BDE is the triangle of its medians.
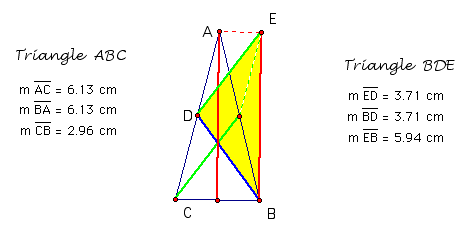
Notice that triangle BDE is also isosceles since ED = BD. This will always be true since two of the medians will always have the same length. These are the medians formed by finding the midpoints of the two equal sides and connecting them to the opposite vertex.
(2) Triangle ABC is a right triangle and triangle BDE is the triangle of its medians.
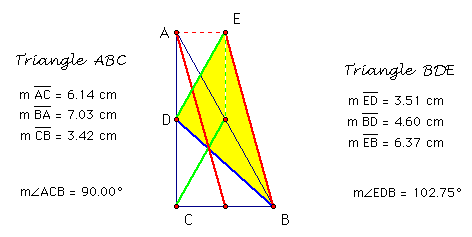
Notice that triangle BDE is not a right triangle. So, a right triangle will not always have a triangle of medians that is also right.
(3) Here are 3 examples of when the original triangle and the medians triangle are both right triangles:
Conclusion: The original triangle and the medians triangle are both right triangles when the angle measurements are 90, 55, and 35 degrees.