

A. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
Click here to work with this GSP file.
B. Conjecture: It seems that the ratio is always 1, no mater the triangle nor the location of P.
Proof:
Part 1: Construct a line parallel to AB through P.
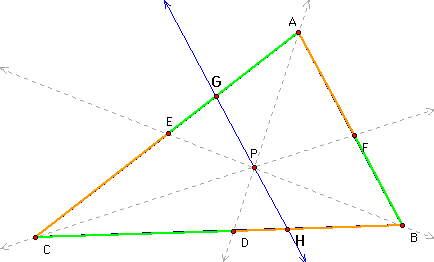
Part 2: Construct a line parallel to BC through P.
Part 3: Construct a line parallel to AC through P.
CONCLUSION:
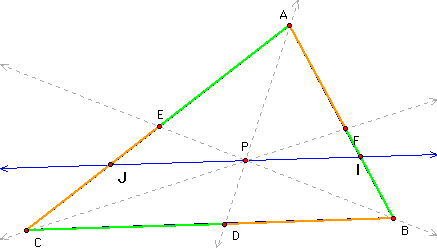
Can the result be generalized (using lines rather than segments to construct ABC) so that point P can be outside the triangle?
A GSP sketch suggests that even if P is outside the triangle, the ratio is still equal to 1.
Click here to work with this GSP sketch.
C. Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?
I will start with the second question. After working with my first GSP sketch [from section A], I found when the ratio of the areas of triangles ABC and DEF is 4, then the points D, E and F are the midpoints of their respective sides (this implies that P is the centroid).
This makes sense because the triangle formed by the midpoints is the medial triangle. By definition the area of a medial triangle, DEF, is 1/4 the area of the original triangle, ABC.
Now, an argument that the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4:
If we move P in our GSP sketch in any direction, the area of triangle DEF gets smaller and makes the ratio larger. So, we want to consider when the area of triangle DEF is maximized to find when the ratio is minimized.
We know that when the ratio equals 4, P is the centroid or the center of gravity for the triangle. If P moves toward vertex A, the area of triangle DEF will decrease and approach zero. The same for if P moves toward vertex B or C. Therefore, when P is the centroid of triangle ABC, the area of triangle DEF is maximized and the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4.