---

---

Exploring the graph of

by

Mindy Swain

Assignment 2

#7. Try several graphs of on the same axes.

(i.e., use different values of a)

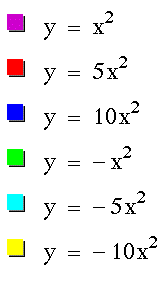
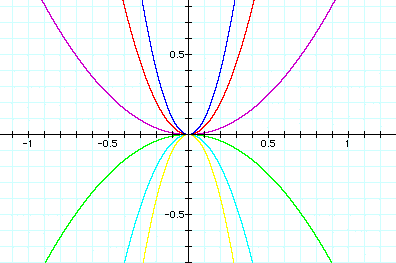
The first observation I noticed about these graphs is that they are all parabolas with vertex at (0,0). Also, I did not graph the case for a = 0 since this would give us the equation y = 0 (the x-axis). For all values of a > 0, the parabola opens upward and for all values of a < 0, the parabola opens downward. Since we have generalized for positive and negative values of a, we can now consider |a|. As |a| increases, the parabola compresses or becomes skinnier. After making these observations, I now would like to consider values 0 < a < 1.

Consider the following graphs for various values of a:

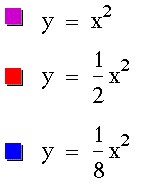
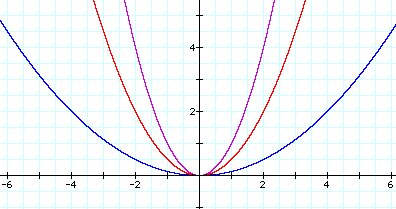
Now I can see that the parabolas for values 0 < a < 1 are more expanded or wider than for a = 1, and as values of a get smaller the parabola gets wider.

Conclusion:

(1) For a = 0, the graph is the x-axis.

(2) For all values of a > 0, the parabola opens upward and for all values of a < 0, the parabola opens downward.

(3) For all values of a not equal to zero, the parabola is expanded when |a| is small and compresses as |a| increases.

Return