
Assignment # 2
By Sharren M. Thomas
In this exploration I will
examine the graph y = ax2 on the same axes for different values of
a.
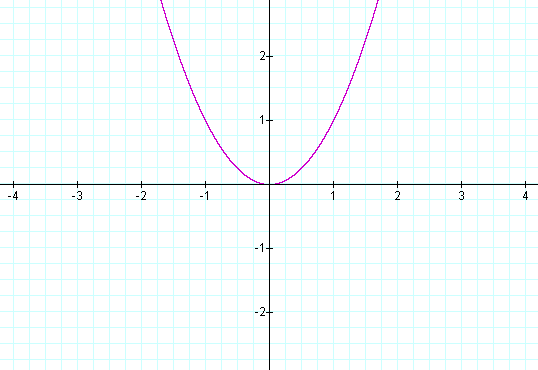
For a =
1; y = x2 is a parabola
whose vertex is at the origin. See the graph below.
![]()
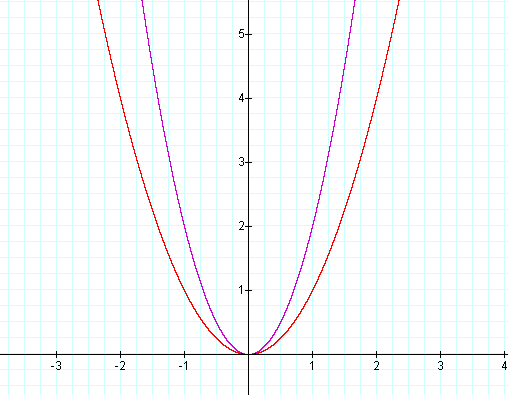
For a = 2; y = 2x2 is a parabola whose
vertex is at the origin, but the graph of the parabola is now stretched
vertically by a factor of 2, each y-coordinate at each point has been
multiplied by 2. See both graphs below.
![]()
![]()
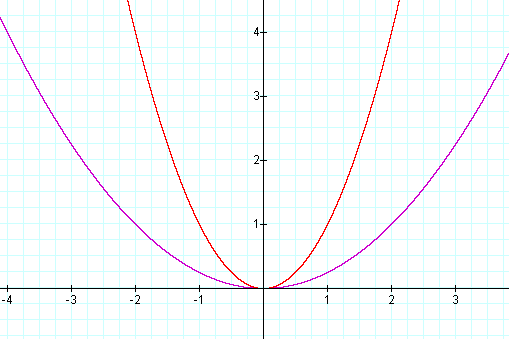
For a =
1/4 y = (1/4) x2 is a parabola
whose vertex is at the origin, but the graph of the
parabola
is now compressed vertically, each y – coordinate at each point
has
been multiplied by 1/4. See both graphs below.
![]()
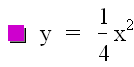
Conclusion:
For y = ax2 with a> 1 the graphs will be parabolas whose vertices are
at the origin that are stretched vertically by a factor of a. Click the movie below. Notice that the
parabolas are becoming more narrow or sharper at the vertices.
For y = ax2 with 0 < a > 1 the graphs will be parabolas whose vertices
are at the origin that are compressed vertically by a factor of a. Click the movie below. Notice that the
parabolas are becoming wider or flatter at the vertices.
For a =
-1; y = -x2 is a parabola whose
vertex is at the origin, but the graph of the parabola has been reflected
across the x-axis. Each y-coordinate of the new graph has been multiplied
by -1. See the graph below.
![]()
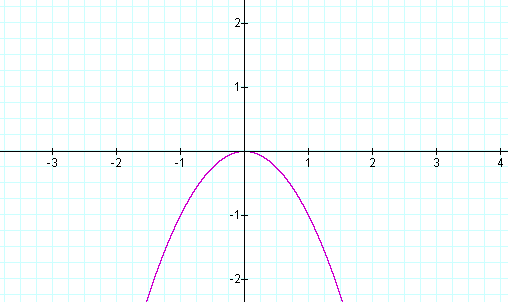
For y = ax2 with a < 0; the graphs will be
parabolas whose vertices are at the origin that are reflected across the
x-axis. When a is a negative
fraction it the graph is both reflected across the x-axis and compressed
vertically by a factor of a.
Click the movie below. Notice that the parabolas are becoming wider or
flatter at the vertices.
For y = ax2 with a <0; the graphs will be parabolas whose vertices are at
the origin that are reflected across the x-axis. When a is a negative integer the graph is both reflected
across the x-axis and stretched vertically by a factor of a. Click the movie below. Notice that the
parabolas are becoming narrow or sharper at the vertices.