
Assignment
3
By:
Sharren M. Thomas
Examine the graphs of
![]()
See below the graph for b = -3, -2, -1, 0, 1, 2, and 3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
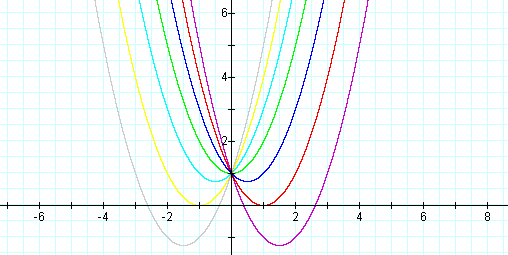
If I find the vertices of each parabola, which can be found by finding the x-coordinate by calculating -b/2a and plugging in the x-value to obtain the y-value. Below see the above graph with the coordinate points for each vertex labeled.
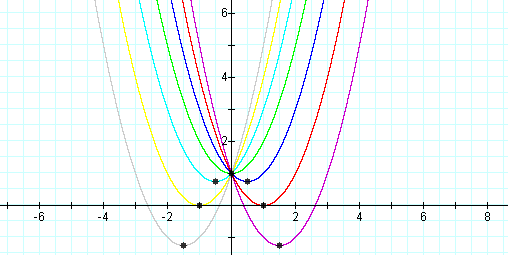
When the points are traced the locus of the
vertices of the set of parabolas show that the locus is the parabola ![]()
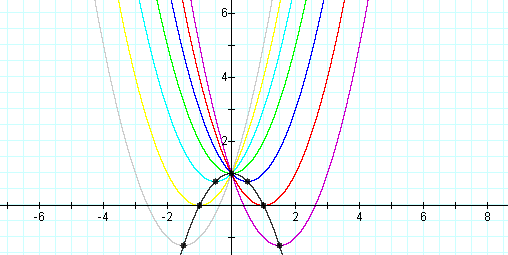
Now let's consider finding the general form of the locus of the vertices for the set of parabolas graphed from
![]()
As you can see above we see that the locus of vertices is a parabola, if we consider the vertex point (0, 1) and (1, 0) which is a point on this parabola; then we using the vertex form
y = a (x - h) + k, where (h, k) are the coordinates of the vertex. So we obtain y = a (x - 0) + 1 and by substituting (1, 0) for (x, y) to find the value of a; we get 0 = a + 1 thus a= -1 and the equation of the parabola is y = -x2 + 1. In general, since (0, c) will always be the vertex of this parabola and its direction is opposite that of the original graphs, then
y = -ax2 + c is the locus of points of the vertices.