
CENTERS OF A TRIANGLE
Sharren M. Thomas
Assignment 4
In a
standard Geometry course, students typically study and often construct points
of concurrency for the Centroid (G), orthocenter (H), Circumcenter (C), and
finally the Incenter (I).
In this
write-up, I will explore with my students the various points G, H, C, and I and
their mathematical relationships in several different triangles. Additionally, we
will explore the Euler line which is the segment joining C, G, and H.
This
comparison will most likely take place after sections in which students have
already learned to classify a triangle according to its sides and angles.
GSP (Geometry Sketchpad) will be used to explore the behavior of these
concurrent points (G, H, C, & I) of a equilateral, right, acute, and
obtuse triangles.
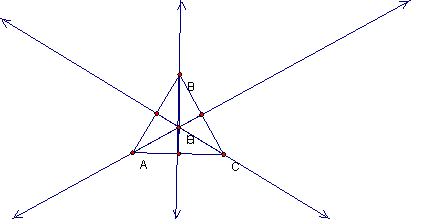
See below,
a triangle which shows the centroid, orthocenter, circumcenter, and the
incenter for the same equilateral triangle. Notice that G, H, C, and I
coincide.
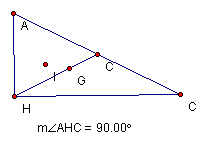
In a right
triangle H, the orthocenter corresponds to the 90º vertex angle. C,
the Circumcenter is located at the midpoint of the hypotenuse, G and I are
located within the triangle. See below.
Now we
will explore the location of these points in an acute (non-equilateral)
triangle.
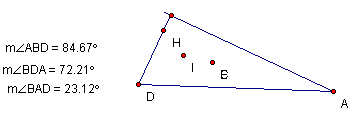
Notice
that all concurrent points lie within the triangle, and the Centroid and the
Circumcenter overlap for this case, but not for all cases of acute triangles.
Last
investigation explores the concurrent points in an obtuse triangle.
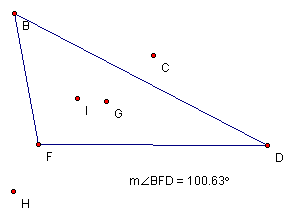
Notice
that both the Circumcenter, C, and the Orthocenter, H, are located outside the
triangle.
Recall, in
a right triangle H lies on a vertex and C lies on the midpoint of the opposite
side; thus, segment HC would be considered a median of the right
triangle. Thus G should be 2/3 the distance from H to C as the
centroid. This a particular properties that holds true. Is G always
2/3 the distance from H to C on the Euler line regardless of whether it is a
right triangle or not.
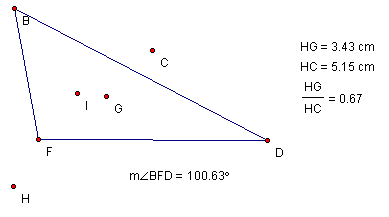
Click here to manipulate the sketch
by moving a vertex and analyze the ratio of HG to HC.