Assignment 6
Sharren M. Thomas
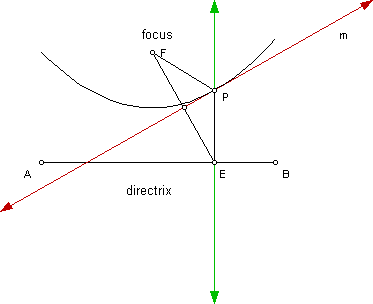
I will construct a parabola given a fixed point, F, the focus and a line (segment) for the directrix. Recall that a parabola is defined in terms of a fixed point, called the focus, and a fixed line called the directrix.
In a parabola, the distance from any point, P, on the parabola to the focus, F, is equal to the shortest distance from P to the directrix.
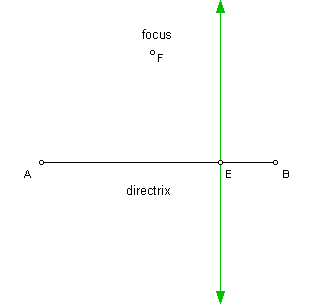
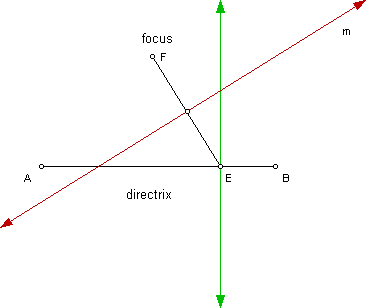
Given a fixed point F for the focus and segment AB for the directrix, I will construct a perpendicular line through the point E on segment AB as shown below I formed segment EF and constructed the perpendicular bisector of this segment (line m):
Find the point of intersection of line m and the green line (call it point P). By connecting segment PF and segment PE, these segments which are congruent sides of the now formed isosceles triangle. Therefore, I have construct a point P equidistant from the focus and the directrix:
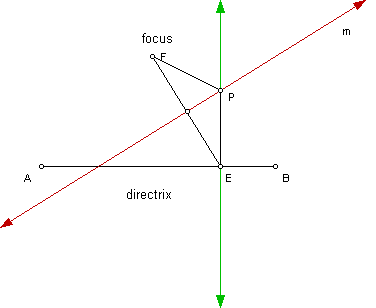
Click here to view animation and trace of point P the resulting parabola will be displayed. Click here to view trace of the tangent line at point P the resulting parabola will be displayed
See below to view the locus of points equidistant from a fixed point, F, the focus and the directrix line, AB, generated by GSP :