Assignment 8
by Sharren M. Thomas
Altitudes and Orthocenters
I will begin
with an exploration of orthocenters that have been constructed inside of a
particular triangle, ABC.
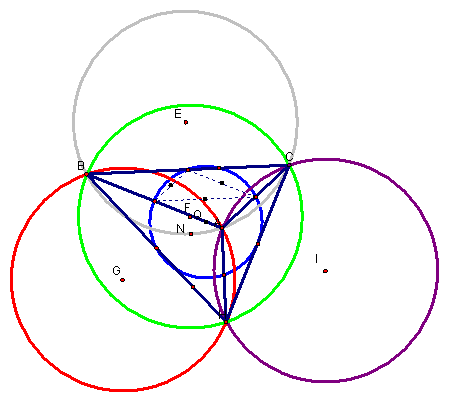
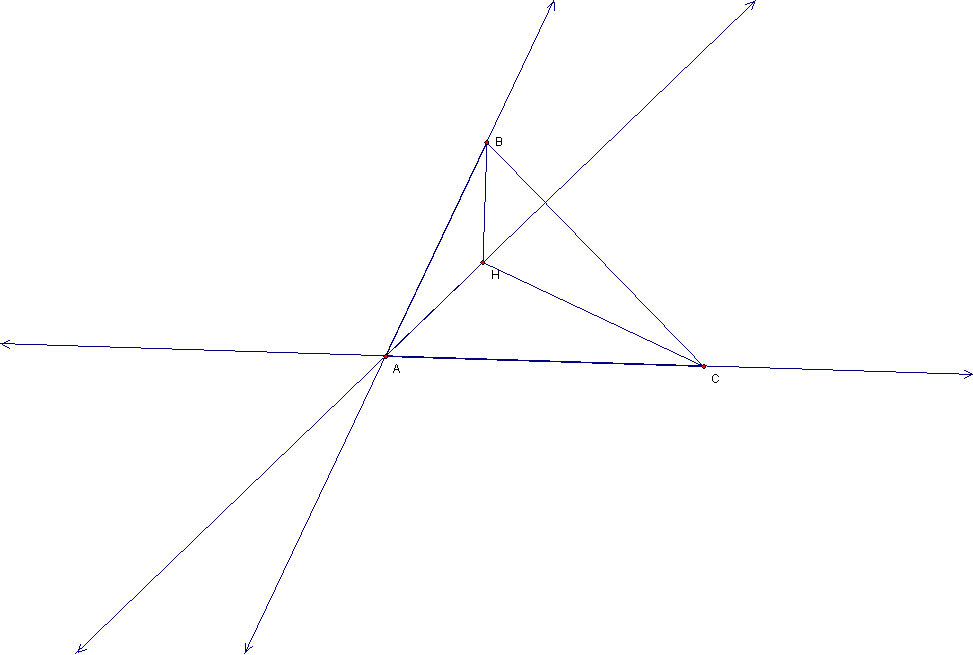
When a triangle
HBC is constructed from a triangle ABC and its orthocenter H. Where will
the orthocenter be located for the new triangle HBC? Let us explore.
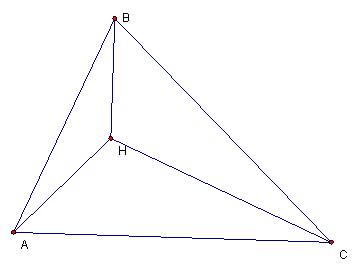
The orthocenter
for HAB is at C. Similarly the Orthocenter for triangle HBC is
located at point A. And the orthocenter for HAC is located at point
B. See below the orthocenter for HAB, HBC, and HAC.
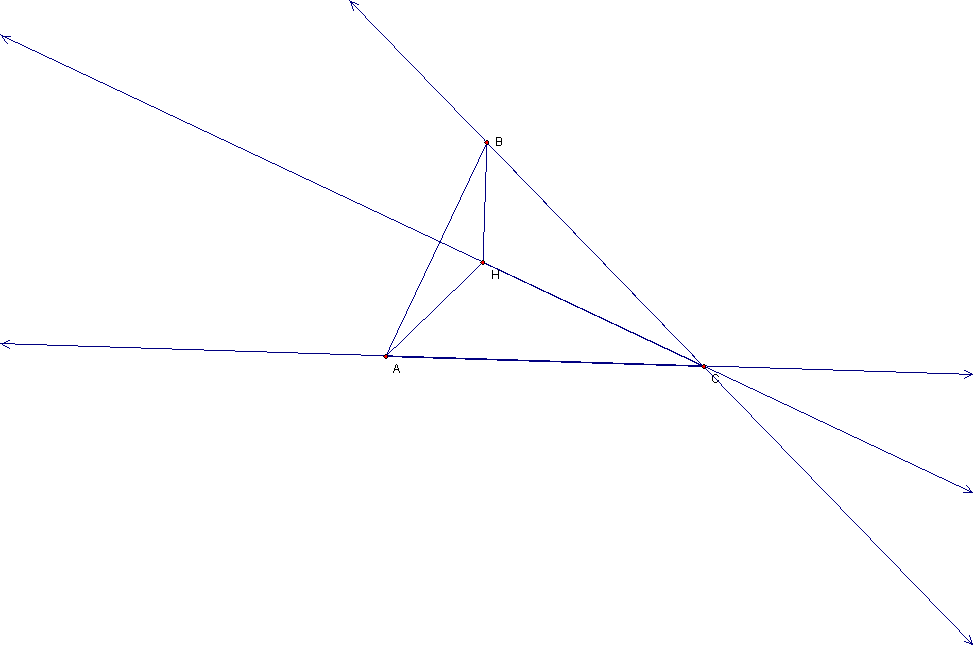
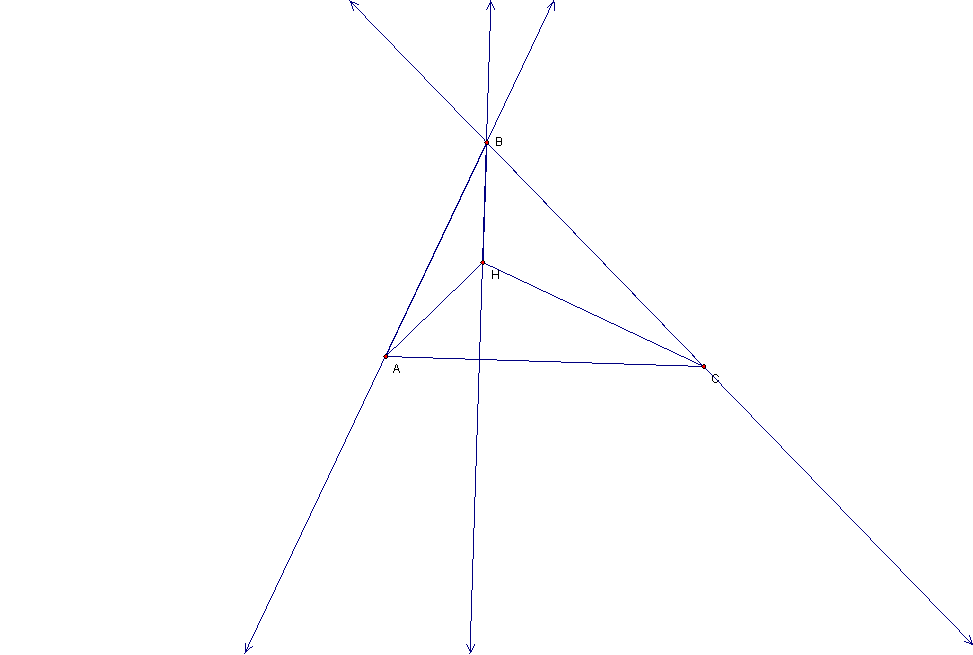
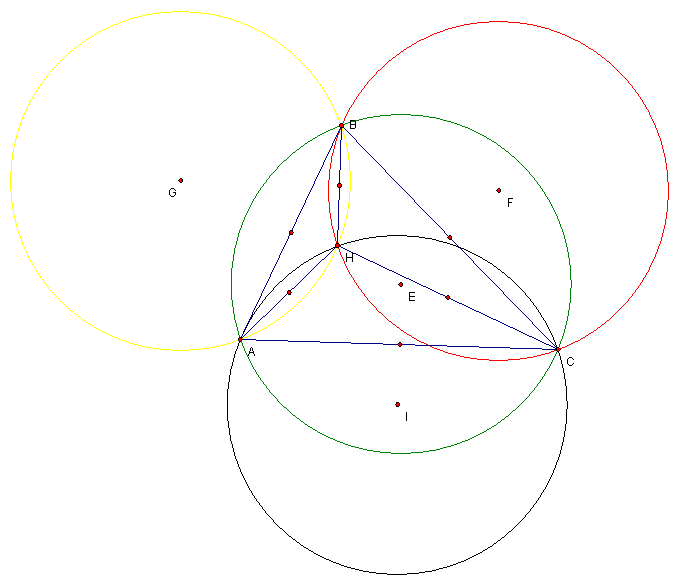
Now I will
begin by constructing the circumcenters of triangles ABC, HBC, HAB, and HAC
which are respectively points E, F, G, and H, see below. I will construct
the CircumCIRCLES for each triangle, also see below.
Now, let's
explore the relationship between the type triangle that ABC is and its
relationship with the previously constructed orthocenters and circumcircles.
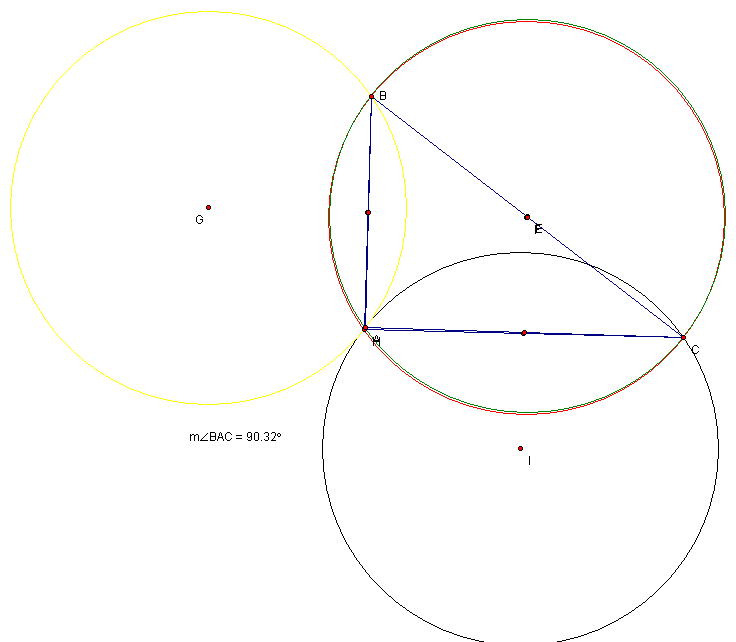
See below that
when triangle ABC is a right triangle, where angle A is the right angle then notice that the
triangle ABC's orthocenter
H, corresponds with the vertex A; which happens to be the circumcenter for
triangle HBC. Thus, triangle ABC and triangle HBC have the corresponding
circumcenters, therefore the circumcircles are the same. If in turn, ABC
is a right triangle with the right angle at vertex B, then circumcenter of ABC,
point H and the circumcenter for triangle HAC point B correspond. n
Similarly, ABC is a right triangle the right angle at vertex C, then
circumcenter, H, or ABC and the circumcenter of HAB, C, will overlap.
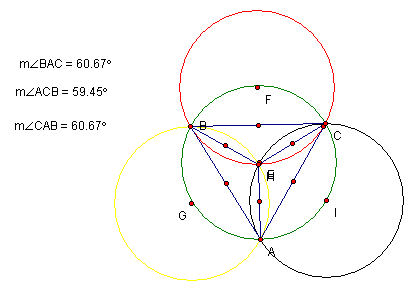
If triangle ABC
is an equilateral triangle, and simultaneously both its orthocenter point H and
its Circumcenter, point E overlap; then the circumcenters of triangle HBC, HAB,
and HAC are points located on triangle ABC's Circumcircle. See below.
Now let's
construct the 9-point circle from this construction. See below, the blue
circle is the 9-point circle.
For a triangle
ABC. The 9-points include the 3 midpoints of the original triangle.
A medial triangle is created from these midpoints. Now, if we construct
the orthocenter of this medial triangle this becomes the center of the 9-point
circle, whose radius is the distance from the orthocenter of the medial
triangle to any midpoint of the original triangle ABC. The 9-point circle
also passes through the perpendicular segments, and the feet of a triangles
perpendicular.