Final Assignment
By Sharren M. Thomas
THE PROBLEM:
A. Consider any triangle ABC. Select a point P inside the triangle and draw
lines AP, BP, and CP extended to their intersections with the opposite sides in
points D, E, and F respectively.
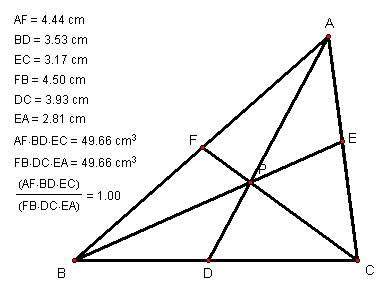
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles
and various locations of P. CLICK HERE to Manipulate the triangle to obtain
various triangles and to analyze for various locations of P.
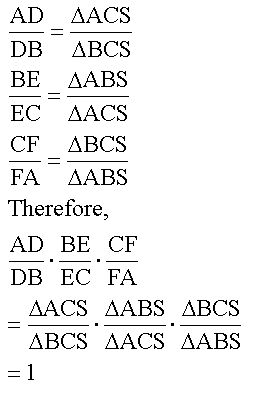
B. Conjecture? Prove it! (you may need draw some parallel lines to produce some
similar triangles) Also, it probably helps to consider the ratio
![]()
Can the result be generalized (using lines rather than
segments to construct ABC) so that point P can be outside the triangle? Show a working GSP
sketch.
It appears that ![]() will
be equal to 1, for various locations of P and for various triangles.
will
be equal to 1, for various locations of P and for various triangles.
I wasn't able to prove this conjecture on my own, but the
following websites gave me assistance with the Ceva Theorem.
http://www.ies.co.jp/math/java/vector/ceva/ceva.html
http://planetmath.org/encyclopedia/CevasTheorem.html
http://www.cut-the-knot.org/Generalization/ceva.shtml
http://www.math.uci.edu/~mathcirc/math194/lectures/advanced3/node2.html
Problem
|
Prove Ceva's Theorem.
|
|
Answer
![]()
|
|
|
C. Show that when P is inside
triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always
greater than or equal to 4. When is it equal to 4?
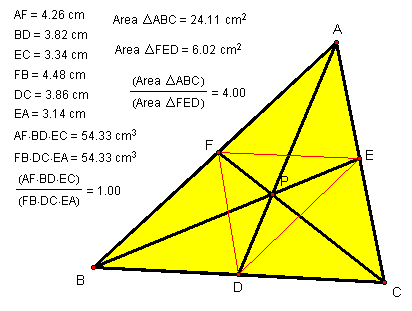
The ratio appears to be
equal to 4 when points D, E, and F are the midpoints of the sides ABC. CLICK HERE TO INVESTIGATE WHEN THE RATIO IS
GREATER THAN 4.