
Department of Mathematics Education
EMAT 6690, J. Wilson
Friday the 13th
By Matt Tumlin
1. Show that for any year there must be at least one
month and at most three months for which the 13th of the month falls on
Friday.
2. Observe that in 1998 both February and March
have a Friday the 13th.
a. Prove
that Friday the 13th can occur in two consecutive months only in February and
March in a year that is not a leap year. On what day of the week must January 1
occur for February and March to have Friday the 13ths?
b. What is
the next year in which this will occur again?
c. Is
there a pattern or cycle by which you can determine which years between 2000
and 2100 that this will occur?
In any year there must be at least one Friday the 13th,
and there can be no more than three. One
way to show this is by using a spreadsheet showing all the possible outcomes
according to the beginning day of the year by using mod 7. To see an example in Excel, click HERE.
As you can see, the first spreadsheet is for any year
that would start on a Monday. It
contains everyday of the year, and this is a lot of information to look through
when you are just interested in 12 Fridays.
A simpler version of the same information is available by just looking
at the 13th day of each month.
To see an example in Excel, click HERE.
Instead of a running total for the day of the year, I
have entered the exact number for the 13th day of each month. This makes the spreadsheet more manageable
and easier to look at.
Next, we need to look at all of the possible years
according to the beginning day of the year.
To see an example in Excel, click HERE.
However, we have not seen all the possible year
outcomes. We have yet to look at the
leap year possibilities. To see an
example in Excel, click HERE.
As you can tell, there is at least one Friday the 13th
a year, two Friday the 13ths in 6 of the years, and three Friday the
13ths in 2 of the years.
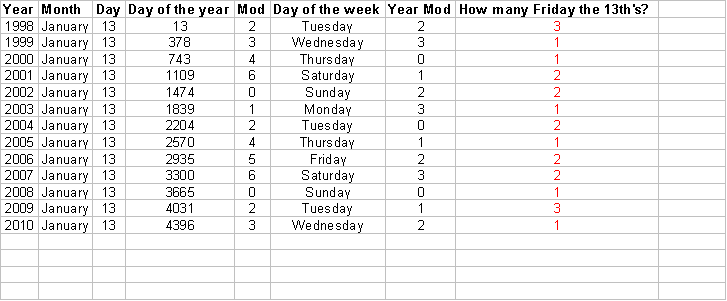
In 1998, both February and March had Friday the 13th. If you go back to the previous spreadsheets,
you see that this only occurs when it is not a leap year and the year begins on
a Thursday. To see if or when this will
occur again, we can set up a spreadsheet that starts with 1998. To see an example in Excel, click HERE.
If you notice, there is a pattern within this
chart. The first year starts on a
Thursday, which was why it contained successive Friday the 13ths. The following year starts on a Friday and the
pattern follows. Each successive year
starts with the next day of the week.
The pattern changes for a leap year
To use the spreadsheet yourself, click HERE.