
Department of Mathematics Education
EMAT 6690, J. Wilson
The
Pipeline Problem
By Matt Tumlin
A common problem encountered
by the oil industry is determining the most cost effective pipeline route in
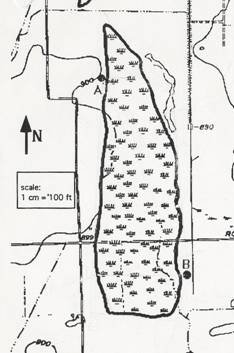
connecting various wells in an oil fertile area. The map below is a section of the U. S.
Geographical Survey Contour Map of northeast
·
Straight, two-inch coated pie must be used at a cost of $1.50/foot.
·
A maximum of two elbow joints may be used. Assume that the elbow joints may be
fabricated with any angle measure.
·
In crossing normal terrain, instillation cost is $1.20/foot.
·
Installation in the wetland area requires an additional Track Hoe at a
cost of $60/hour.
·
In a 10 hour day, a Track Hoe can dig approximately 300 foot trench.
Determine the pipeline route
connecting the new well at A to the well at B, which incurs the least cost.
For a printable Microsoft
Word version, CLICK HERE.
Suggestions: First, solve the problem as if the wetland
separating A and B were a rectangle, and then improve on this solution by
modeling the wetland area more accurately.
Also, reduce the number of paths to consider before you begin modeling. For example, one need not consider a path
around the swamp to the north since it is further than the path around the
swamp to the south and both traverse only normal terrain.
Problem posted by John
Ramsay,
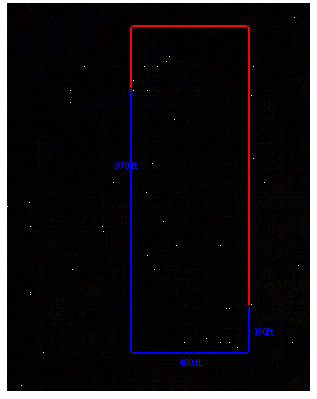
Rectangular Model
We can first begin to solve
this problem by using a rectangle as a model for our wetland. The rectangle we used has five separate
measurements.

A. The distance from A to the southern most point of the
wetland.
B. The vertical distance from B to the point perpendicular
to A (also the vertical distance form A to the point perpendicular to B).
C. The width of the wetland.
D. The distance from A to northern most part of the
wetland.
E. The distance from B to the southern most part of the
wetland.
By using these measurements, we can find a cost
equation for a route the pipeline can take through our model. Once we get this equation, we can find the
route which incurs the minimum cost.
Our cost function is:
![]()
The variable, x, is the total distance on normal
terrain. This formula is deducted
through many steps. To follow the steps
I used, CLICK HERE.
By minimizing this equation, we can find the cheapest
route through our rectangle model, which is $3644.83. To follow the steps I used, CLICK HERE.
 Other Routes
for the Rectangular Model
Other Routes
for the Rectangular Model
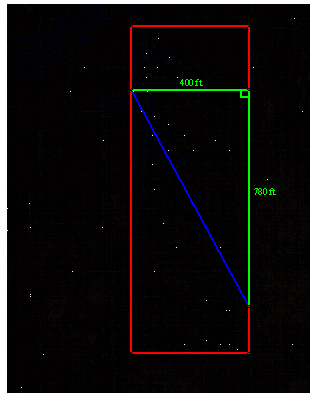
The southern route around the wetland is the total
distance around the wetland.
This is 970 ft + 190 ft + 400 ft, which equals 1560
ft. We multiply that by 2.7, which is
the total cost per foot on normal terrain.
970 + 190 + 400 = 1560
1560(2.7) = $4212.00
The total cost of this route is $4212.00, and since this
is more expensive than our minimum cost for the rectangular function, this is
not the route we want. The northern
route is more expensive because it was given that the northern route was longer
than the southern route, thus is would cost more.
A direct route through the wetland area can be found
by using our rectangle cost function just by using zero for x, since there is
no distance traveled on normal terrain.
![]()
![]()
![]()
This is also more expensive than our minimum cost.
The cheapest way through the wetland alone is a
straight line from A to B because the shortest distance between two points is a
straight line. Thus, any routes through the
wetland alone with one or two elbow joints will cover more wetland and
therefore be more expensive.
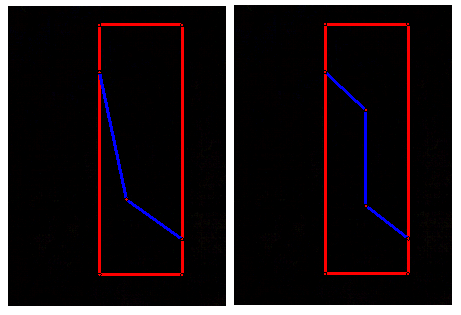
Other possible routes might be as follows:

See if you can find a cheaper price.
Trapezoidal Model
Since we now have the cheapest route thru our
rectangular model, we can begin to remodel the region to more closely resemble
the actual wetland area.

By using a trapezoid as the model for the wetland, we
get closer the shape of the wetland because the eastern side tends to indent toward
the north-west.
My model has the following dimensions (which were
found by measuring the map):
A. The distance from A to the southern most point of the
wetland.
B. The distance from B north to the point created by the angled
portion of the trapezoid on the eastern side.
C. The width of the wetland.
D. The distance from A north to the point created by the
angled portion of the trapezoid on the western side.
E. The distance from B to the southern most part of the
wetland.
F. The distance from the northern most point on the
western side to the northern most point on the eastern side of the model.
Q. The measure of
the northern angle in the trapezoid.
For the trapezoid model, the cost function is:
![]()
The variable, x, is the distance from the northern
most point in the western side to the point created where the pipeline
intersects the angled side. This formula
is deducted through many steps. To
follow the steps I used, CLICK HERE.
By minimizing this function we can find the minimum
cost, which is $3245.55. To follow the
steps I used, CLICK HERE.
This equation does basically every logical path. However, any path in the trapezoid that does
not emerge on the angled portion, in other words, x>1030, can be used in the
rectangle model.
For example:
In conclusion, the cheapest route is the one found
with the use of the trapezoid model.
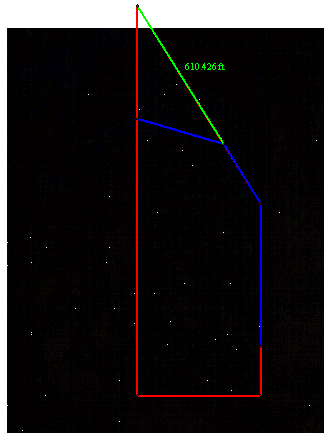
The cost of this route is $3245.55.
Return
to Matt’s EMAT 6690 Page