
Department of Mathematics Education
EMAT 6700, J. Wilson
J. Matt Tumlin
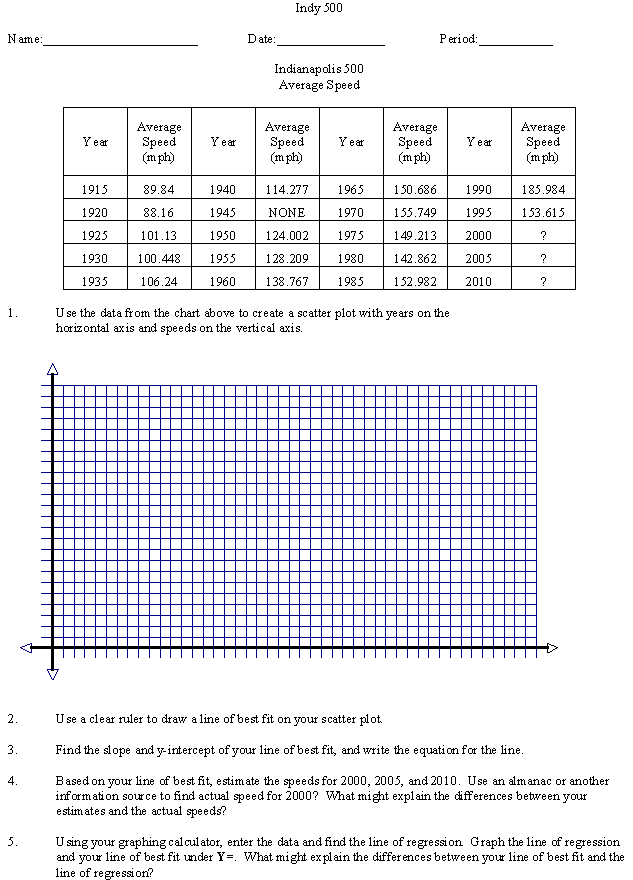
The average speeds at the
To motivate the students, discuss the data for the Indy 500
race. Ask students what accounts for the
obvious increase in speed over the years.
Encourage students who are familiar with automobile racing to share some
of their technical knowledge.
Ask students what they envision for the future. Do they think the speeds will increase
steadily? Do they think there will come
a time when the speeds will level off?
Do they think some technological advance will cause a dramatic increase
in speeds?
For a Microsoft Word copy, CLICK HERE.
Directions
You can have students can work in pairs. For questions 1-4, each student should draw the scatter plot and determine a line of best fit. The partners can then compare lines of best fit to see how closely they match. Why is theirs different from their partners? Stress the fact that when using this technique, the lines of best fit are approximations. There is no one right answer. They can use the Internet to find the actual speed of the 2000 race.
Using the calculator
is optional. In higher classes, the
students should be familiar with the graphing calculator. In lower classes, this would be a good way to
introduce it. For
question 5, the students can work together to determine the correct calculator
procedure for finding the regression equation.
Be sure the students understand that the calculator uses a well-defined
algorithm, so this time, there will be only one right answer.
This problem has many aspects you can go into, slope,
y-intercept, equation of a line, and use of technology. It also has many entry and exit points.