Department of Mathematics Education
EMAT 6700, J. Wilson
Number Trick
J. Matt Tumlin
Students will use the composite of f and g, f(g(x)),
to model a familiar computational game.
They will further investigate composition in relation to the graphs of
parent functions.
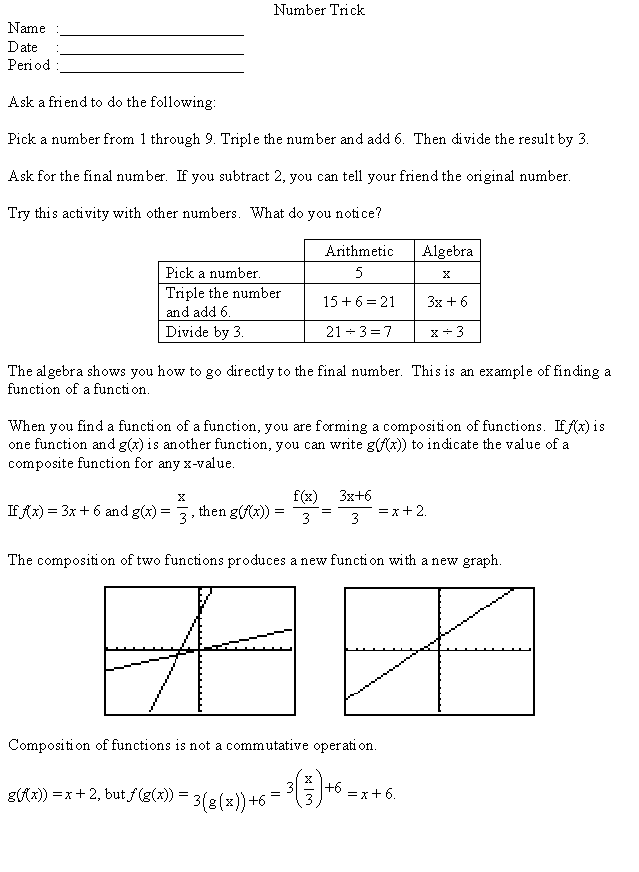
To motivate the students, play the number game on one
student. Ask how you derived at the
answer without knowing the original number.
Have the students examine the table near the top of the page and explain
how the entry x + 2 was derived.
Have students make changes in the steps to see how the expression x
+ 2 is affected.
Directions
You can have students can work in pairs. However, for question 1, each student should
develop their own two step computational game.
The partners can then play the games to determine if the outcomes are as
expected. Stress the fact that when
completing this activity, there is no one right answer.
For questions 2 and 3, the students can work together to
determine the domains and ranges. One
partner can then fill in the table, while the other partner graphs the composition. The two can switch roles for question 4.
This activity has many aspects you can go into, evaluating
functions, composition of functions, function computation, graph translations,
domain, range, inverses, and use of technology.
It also has many entry and exit points.